Comenzamos tema nuevo donde nuestro cometido será estudiar las funciones \[f:D\subset\mathbb{R}^n\longrightarrow\mathbb{R}^m,\] para \(m,n\geqslant 1\). Si \(m=n=1\), tenemos las funciones reales de una variable real que conocemos habitualmente. Cuando \(n=1\) y \(m>1\) la denominamos función vectorial de una variable real.
Sin embargo, trataremos con mayor asiduidad en el caso de que \(n>1\). De este modo, las funciones del tipo \[f:D\subset\mathbb{R}^n\longrightarrow\mathbb{R}\] se denominan funciones reales varias variables, o campos escalares; y las \[f:D\subset\mathbb{R}^n\longrightarrow\mathbb{R}^m,\] con \(m>1\), se denominan función vectorial de varias variables, o campo vectorial.
Vamos a introducirnos en los campos escalares, comenzando con los de dos variables:
Una función \(f\) de dos variables es una regla que asigna a cada par ordenado de números reales \((x, y)\) de un conjunto \(D\), un único número real que se denota con \(f(x, y)\).
El conjunto \(D\) es el dominio de \(f\) y su rango es el conjunto de valores que toma \(f\), es decir, {\(f(x,y);(x,y)\in D\)}.
A menudo, escribimos \(z=f (x, y)\) para hacer explícito el valor que toma \(f\) en el punto \((x, y)\). Las variables \(x\) y \(y\) son variables independientes y \(z\) es la variable dependiente. \(z=f (x, y)\) y \(u=f (x, y,z)\) son los campos escalares que trabajaremos. En matemáticas y física, un campo escalar representa la distribución espacial de una magnitud escalar, asociando un valor a cada punto del espacio. En matemáticas, el valor es un número; en física, una magnitud física.
Curvas de nivel
Si nosotros grafiamos los puntos \((x,y,f(x,y))\in\mathbb{R}^3\), tenemos la representación de los valores de \(z=f (x, y)\) como una superficie en \(\mathbb{R}^3\). Si hacemos fijo \(z\) nos define la curvas de nivel:
Las curvas de nivel de una función \(f\) de dos variables son las curvas cuyas ecuaciones son \(f (x, y)=k\), donde \(k\) es una constante (en el rango de \(f\)).
Las curvas de nivel son justamente las curvas de la gráfica de \(f\) en el plano horizontal \(z=k\) proyectadas en el plano \(xy\). Si dibuja las curvas de nivel de una función y las imaginamos como elevaciones de la superficie a la altura indicada, entonces puede formar mentalmente una imagen de la gráfica. La superficie tiene pendiente abrupta donde las curvas de nivel están muy cercanas entre sí. Es algo más plana donde las curvas se separan.
By <a href=»//commons.wikimedia.org/wiki/User:MHz%60as» title=»User:MHz`as»>MHz`as</a> – <a href=»//commons.wikimedia.org/wiki/File:Contour2D.jpg» title=»File:Contour2D.jpg»>Contour2D.jpg</a>, CC BY-SA 3.0, Link
El mismo proceder nos sirve para extender estas definiciones a tres o más variables.
Las curvas de nivel nos son útiles para aproximar valores que desconocemos
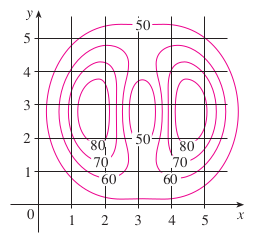
Ejemplo: Un mapa de curvas de nivel de una función \(f\) se ilustra abajo.
Úselo para estimar los valores de \(f (1, 3) \) y \(f (4, 5) \).
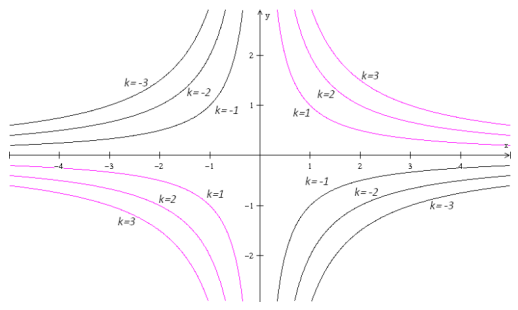
Ejemplo: Dibujar las curvas de nivel para \(f(x,y)=xy\) con valores de \(k=1,-1,2,2\).
Propiedades
- Las curvas de nivel de un campo escalar de dos variables son líneas que conectan puntos con el mismo valor de la función.
- Las curvas de nivel pueden ser utilizadas para visualizar la topografía de una función.
- En un campo escalar radialmente simétrico, las curvas de nivel son círculos concéntricos.
- Las curvas de nivel cerradas pueden indicar la presencia de un máximo o mínimo local.
- El valor de la función es constante a lo largo de una curva de nivel.
- Las curvas de nivel no pueden cruzarse entre sí.
Límite y continuidad de un campo escalar
El siguiente paso, con el que concluiremos la sesión, es formular la definición de límite y continuidad de un campo escalar.
De manera genérica, si \(f:D\subset\mathbb{R}^n\longrightarrow\mathbb{R}\), considerando \(\mathbb{R}^n\) como es \(\mathbb{R}\)-espacio vectorial con el producto escalar euclídeo conocido, decimos que el límite de \(f(x_1,…,x_n)\) cuando \(\vec{x}=(x_1,…,x_n)\) tiende a \(\vec{a}=(a_1,…,a_n)\) es \(L\), y escribimos,
\[\lim_{\vec{x}\to\vec{a}}f(\vec{x})=L\]
si \(\vec{x}\in D\) y \(||\vec{x}-\vec{a}||<\delta\), entonces \(|f(\vec{x})-L|<\epsilon\).
Y será continua si
\[\lim_{\vec{x}\to\vec{a}}f(\vec{x})=f(\vec{a}).\]
Derivadas parciales
Como las derivadas en una variable, las derivadas parciales están definidas como el límite. Donde U es un subconjunto abierto de \(\mathbb{R}^n\) y \(f:U\to\mathbb{R}\) una función. Definimos derivada parcial de f en el punto \(\mathbf{{a}}=(a_1,a_2,\ldots,a_n)\) con respecto a la \(i-\)ésima variable xi como:
\[\frac{ \partial }{\partial x_i }f(\mathbf{a}) = \lim_{h \rightarrow 0}{ f(a_1, \dots , a_{i-1}, a_i+h, a_{i+1}, \dots ,a_n) – f(a_1, \dots ,a_n) \over h }\]
En realidad, las parciales es una particularización de las derivadas direccionales, ya que estas son derivadas direccionales en los vectores paralelos a los ejes.
Ejemplo: Sea \(f(x,y)=x^2+xy+y^3\), ¿cuál es el valor de \(\frac{\partial f}{\partial y}(1,1)\) ?
Ejemplo: Sea \(f(x,y)=\sin(x^2+y)-xy\). ¿Cuánto vale \(f_x(1,1)+f_y(1,1)\)?
Propiedades
Bibliografía
- Capítulo 13 del libro Cálculo de varias variables, de James Stewart.
|
Ejercicio: Sea \(f(x,y)=\frac{x}{(x+y)^2}\). ¿Cuánto vale \(f_x(1,1)+f_y(1,1)\)? |