Al hablar de grupos se introdujo la definición de homomorfismo y con ella la de núcleo. Ahora extendemos esta definición a espacios vectoriales para definir la aplicación lineal: un homomorfismo entre espacios vectoriales. Así diremos que una aplicación (en algunos libros le dicen Transformación) entre dos espacios vectoriales, \(f:V\to W\), sobre el mismo cuerpo\(\mathbb{K}\), es lineal si se cumple que para todo par de vectores \(\vec{v},\vec{u}\in V\) y todo par de escalares \(\lambda,\mu\in\mathbb{K}\) se verifica que: \[f(\lambda\vec{v}+\mu\vec{u})=\lambda f(\vec{v})+\mu f(\vec{u}).\]
Para este tema podéis consultar el capítulo 6 del libro ÁLGEBRA LINEAL Definiciones, Teoremas y Resultados, Juan De Burgos Román, ingebook
Ejercicio: Sea la aplicación \(tr:\mathcal{M}_2(\mathbb{R})\to\mathbb{R}\) dada por \[tr\begin{bmatrix}a & b \\
c & d\end{bmatrix}=a+d,\] ¿es lineal?
Ejercicio: Sea la aplicación \(f:\mathbb{R}^3\to\mathcal{M}_2(\mathbb{R})\) dada por \[f(x,y,z)=\begin{bmatrix}x & y \\ z & x\end{bmatrix}\] ¿es lineal?
Ejercicio: Sea la aplicación \(f:\mathbb{R}_2[X]\to\mathbb{R}_2[X]\) dada por \[\forall p\in\mathbb{R}_2[X];\ f(p(X))=1-p(X)-\frac{d}{dX}p(X)\] ¿es lineal?
Matriz asociada a un aplicación lineal
Dada una aplicación lineal, \(f:V\to W\), entre dos espacios vectoriales finitamente generados sobre el mismo cuerpo \(\mathbb{K}\), con \(\mathbf{dim}(V)=n\) y \(\mathbf{dim}(W)=m\) entonces existe una matriz \(M\in\mathcal{M}_{m\times n}(\mathbb{K})\) tal que \[\forall \mathbf{v}\in V;\ f(\mathbf{v})\sim M\mathbf{v}\]
Esta equivalencia se puede ver en el siguiente diagrama:
\[\begin{matrix}
f:V &\rightarrow & W \\
\downarrow & & \downarrow \\
M:\mathbb{K}^n & \rightarrow & \mathbb{K}^m \\
\end{matrix}\]
Dada una aplicación lineal, \(f:V\to W\), entre dos espacios vectoriales definimos la matriz asociada de la aplicación respecto de una base \(B_V\subseteq V\) como la matriz cuyas columnas son las coordendas respecto de otra base \(B_W\subseteq W\) de las imágenes de los vectores de \(B_V\); es decir, si \(B_V=\{\vec{v}_1,\ldots,\vec{v}_n\}\), \(B_W=\{\vec{w}_1,\ldots,\vec{w}_m\}\), y
\[
\begin{matrix}
f(\vec{v}_1)=k_{11}\vec{w}_1+k_{21}\vec{w}_2+k_{31}\vec{w}_3+\ldots+k_{m1}\vec{w}_m;\\
f(\vec{v}_2)=k_{12}\vec{w}_1+k_{22}\vec{w}_2+k_{32}\vec{w}_3+\ldots+k_{m2}\vec{w}_m;\\
f(\vec{v}_3)=k_{13}\vec{w}_1+k_{23}\vec{w}_2+k_{33}\vec{w}_3+\ldots+k_{m3}\vec{w}_m;\\
\vdots \quad \vdots \quad \vdots\\
f(\vec{v}_n)=k_{1n}\vec{w}_1+k_{2n}\vec{w}_2+k_{3n}\vec{w}_n+\ldots+k_{mn}\vec{w}_m;
\end{matrix}
\]
llamamos matriz asociada de \(f\), a la matriz
\[
M_f=\begin{bmatrix}
k_{11} & k_{12} & k_{13} &\ldots & k_{1n}\\
k_{21} & k_{22} & k_{23} &\ldots & k_{2n}\\
k_{31} & k_{32} & k_{33} &\ldots & k_{3n}\\
\vdots & \vdots & \vdots & \ldots & \vdots \\
k_{m1} & k_{n2} & k_{n3} &\ldots & k_{mn}\\
\end{bmatrix}
\]
Ejercicio: Sea la aplicación lineal \(f:\mathbb{R}^4\to\mathbb{R}^4\) dada por \[f(x,y,z,t)=(x-y+t,y+3x-z,t-2x+y,t+z-y).\] ¿Cuál es la traza de la matriz asociada?
Ejercicio: Sea la aplicación lineal \(f:\mathbb{R}^3\to\mathbb{R}^2\) dada por \[f(x,y,z)=(x-y,y+3x-z).\] Sea la matriz asociada \(M_f\) respecto de la base \(B=\{(1,1,0),(0,-1,1),(3,1,1)\}\). ¿Cuál es la traza de \(M_f.M_f^t\)?
Ejercicio: Sea la aplicación lineal \(f:\mathbb{R}_2[X]\to\mathbb{R}_2[X]\) dada por \[\forall p(X)\in\mathbb{R}_2[X];\ f(p(X))=p(X)-\frac{d}{dX}p(X).\] ¿Cuál es la traza de la matriz asociada \(M_f\) respecto de la base \(B=\{1,1-X,1-X^2\}\)?
Acabamos de ver como una matriz puede representar una aplicación lineal. De hecho podemos establecer una aplicación entre el conjunto de aplicaciones lineales entre dos \(\mathbb{K}\)-espacios vectoriales \(V\) y \(W\), de dimensiones \(n\) y \(m\) (respectivamente) y el espacio vectorial de las matrices \(M_{m\times n}(\mathbb{K})\) que sea un isomorfismo de espacios vectoriales; es decir, una aplicación lineal biyectiva. Esto nos equipara las operaciones con aplicaciones a las operaciones con sus matrices asociadas.
Sabemos que si \(M_f\) es la matriz asociada a la aplicación lineal \(f:V\to W\), entonces
\[f(v_1,v_2,\ldots,v_n)=(w_1,w_2,\ldots,w_m)\Leftrightarrow M_f \begin{pmatrix}v_1\\v_2\\ \vdots\\v_n\end{pmatrix}=\begin{pmatrix}w_1\\w_2\\ \vdots\\w_n\end{pmatrix}.\]
Esto nos permite deducir propiedades de la aplicación con sus correspondientes en la matriz. Por ejemplo, una aplicación lineal entre dos espacios vectoriales de la misma dimensión es un isomorfismo si, y solo si, su matriz asociada es regular.
Así, podemos considerar la matriz asociada a una aplicación lineal, \(f:V\to W\), entre dos espacios vectoriales respecto de una base \(B_V\subseteq V\) como la matriz cuyas columnas contiene las coordenadas respecto de otra base \(B_W\subseteq W\) de las imágenes de los vectores de \(B_V\).
Ejemplo
Ejercicio: Sea \(S=\left\{\begin{bmatrix}a&a-b\\b-a&a+b\end{bmatrix};a,b\in\mathbb{R}\right\}\), determinar una base del subespacio vectorial.
Matriz del cambio de base
¿Y si cambiamos las bases? Es decir, si tengo nuevas bases \(B’_V\) y \(B’_W\), y deseo encontrar la relación entre la matriz asociada aplicación \(M_{f_{B_VB_W}}\), y la matriz \(M_{f_{B’_VB’_W}}\). Veamos primero que ocurre cuando dentro de un mismo espacio vectorial cambiamos la base.
Recordemos que todo espacio vectorial finitamente generado tiene una base. Sea \(V\) nuestro \(\mathbb{K}\)-espacio vectorial y \(\mathcal{B}=\{\vec{v}_1,\ldots, \vec{v}_n\}\), una base del mismo. Para cualquier vector de \(V\), \(\vec{v}\in V\), existirán unos únicos escalares \(k_i\in \mathbb{K}\), tales que \[\vec{v}=k_1\vec{v}_1+k_2\vec{v}_2+\cdots+k_n\vec{v}_n.\] Pues bien, a esos escalares los denominamos coordenadas de \(\vec{v}\) respecto de la base \(\mathcal{B}\). Así, representado mediante sus coordenadas, expresamos que \[\vec{v}=\begin{bmatrix}k_1\\ k_2\\ \vdots \\ k_n\end{bmatrix}_\mathcal{B}\]
Qué ocurre si tenemos otra base \(\mathcal{B}’\), entonces las coordenadas de \(\vec{v}\) serán otras, pero habrá una relación entre ambas. Vamos a utilizar las matrices para encontrar la relación entre ambas coordenadas.
Cuando tenemos dos bases podemos calcular cómo pasar de las coordenadas de una base a la otra. Para ello utilizamos la matriz del cambio de base.

Veamos cómo podemos calcular esta matriz del cambio de base. Sólo tenemos que darnos cuenta como representamos los vectores respecto de cada base. Pongamos dos bases \(B=\{\vec{v}_1,\vec{v}_2,\ldots,\vec{v}_n\}\) y \(B’=\{\vec{u}_1,\vec{u}_2,\ldots,\vec{u}_n\}\). Que un vector cualquiera \(\vec{w}\) tenga por coordenadas \((c_1,c_2,\ldots,c_n)_{B}\) respecto de la base \(B\) significa que \[\vec{w}=c_1\vec{v}_1+c_2\vec{v}_2+\ldots+c_n\vec{v}_n\]
Si cada \(\vec{v}_i\) tiene por coordenadas respecto de una base canónica \((v_{1i},v_{2i},\ldots,v_{ni},)\), podemos escribir lo anterior en forma matricial:
\[\vec{w}=\begin{bmatrix} v_{11} &v_{12}&v_{13}&\cdots &v_{1n}\\ v_{21} &v_{22}&v_{23}&\cdots &v_{2n}\\ \vdots & \vdots & \vdots &\cdots & \vdots\\
v_{n1} &v_{12}&v_{13}&\cdots &v_{1n}\\ \end{bmatrix}\begin{bmatrix}c_1\\c_2\\c_3\\ \vdots \\c_n \end{bmatrix}_{B}\]
Del mismo modo que \(\vec{w}\) tenga por coordenadas \((c’_1,c’_2,\ldots,c’_n)_{B’}\) respecto de la base \(B’\) significa que
\[\vec{w}=c’_1\vec{u}_1+c’_2\vec{u}_2+\ldots+c’_n\vec{u}_n\]
Escrito en forma matricial
\[\vec{w}=\begin{bmatrix}
u_{11} &u_{12}&u_{13}&\cdots &u_{1n}\\
u_{21} &u_{22}&u_{23}&\cdots &u_{2n}\\
\vdots & \vdots & \vdots &\cdots & \vdots\\
u_{n1} &u_{12}&u_{13}&\cdots &u_{1n}\\
\end{bmatrix}\begin{bmatrix}c’_1\\c’_2\\c’_3\\ \vdots \\c’_n \end{bmatrix}_{B’}\]
La igualdad de ambos productos nos ofrece la posibilidad de conocer las coordenadas de un vector una base respecto de la otra:
\[\begin{bmatrix}
v_{11} &v_{12}&v_{13}&\cdots &v_{1n}\\
v_{21} &v_{22}&v_{23}&\cdots &v_{2n}\\
\vdots & \vdots & \vdots &\cdots & \vdots\\
v_{n1} &v_{12}&v_{13}&\cdots &v_{1n}\\
\end{bmatrix}\begin{bmatrix}c_1\\c_2\\ \vdots \\c_n \end{bmatrix}_{B}=\begin{bmatrix}
u_{11} &u_{12}&u_{13}&\cdots &u_{1n}\\
u_{21} &u_{22}&u_{23}&\cdots &u_{2n}\\
\vdots & \vdots & \vdots &\cdots & \vdots\\
u_{n1} &u_{12}&u_{13}&\cdots &u_{1n}\\
\end{bmatrix}\begin{bmatrix}c’_1\\c’_2\\ \vdots \\c’_n \end{bmatrix}_{B’}\]
Si el sistema matricial lo escribimos así: \(P\, C_{B}=Q\,C’_{B’}\), tendremos
\[C_{B}=(P^{-1}Q)\,C’_{B’},\] o \[(Q^{-1}P)\,C_{B}=C’_{B’}.\]
A la matriz \(Q^{-1}P\), la llamamos matriz del cambio de bases de \(B\) a \(B’\), y la notamos como \[C_{BB’}=Q^{-1}P.\]
Como se observa \(C_{B’B}\) es la inversa de \(C_{BB’}\).
Ejemplo
Démosle la vuelta a lo dicho antes y supongamos que ahora deseamos expresar el vector \((-3,1,2)\), dado en la base canónica de \(\mathbb{R}^3\), en sus coordenadas respecto de la base \(B=\{(1,1,1),(1,1,0),(1,0,-1)\}\). La matriz que expresa cualquier coordenada dada respecto de \(B\) en la base canónica es:
\[M_B=\begin{bmatrix}1 & 1 & 1\\ 1 & 1 & 0\\ 1 & 0 & -1\end{bmatrix}.\] Luego buscamos \((a,b,c)\) tal que
\[\begin{bmatrix}1 & 1 & 1\\ 1 & 1 & 0\\ 1 & 0 & -1\end{bmatrix}\begin{bmatrix}a\\ b\\ c\end{bmatrix}=\begin{bmatrix}-3\\ 1\\ 2\end{bmatrix}.\]
Nos basta con
\[\begin{bmatrix}1 & 1 & 1\\ 1 & 1 & 0\\ 1 & 0 & -1\end{bmatrix}^{-1}\begin{bmatrix}-3\\ 1\\ 2\end{bmatrix}=\begin{bmatrix}-2\\ 3\\ -4\end{bmatrix};\]
Es decir, \[-2(1,1,1)+3(1,1,0)-4(1,0,-1)=(-3,1,2).\]
Supongamos que \((2,-1,4)\), está dado respecto de la base \(B^\prime=\{(1,-1,2),(0,2,1),(-1,0,1)\}\), entonces las coordenadas de \((2,-1,4)\) respecto de la base \(B\) serán
\[\begin{bmatrix}1 & 0 & -1\\ -1 & 2 & 0\\ 2 & 1 & 1\end{bmatrix}\begin{bmatrix}1 & 1 & 1\\ 1 & 1 & 0\\ 1 & 0 & -1\end{bmatrix}^{-1}\begin{bmatrix}2\\ -1\\ 4\end{bmatrix}=\begin{bmatrix}9\\ -13\\ 2\end{bmatrix};\]
Para calcular la matriz del cambio de bases podemos utilizar un resultado que nos dice: si a la matriz ampliada \([Q|P]\) le hacemos transformaciones elementales por fila, de modo que obtengamos
\[[Q|P]\to [I_n|C],\]
entonces la matriz \(C=C_{BB’}\).
Matriz del cambio de base para aplicaciones
Ahora veamos cómo afecta el cambio de base entre la matriz asociada aplicación \(M_{f_{B_VB_W}}\), y la matriz \(M_{f_{B’_VB’_W}}\). Esta relación nos la ofrece el siguiente gráfico:
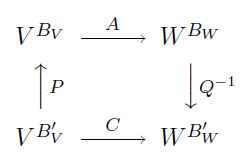
En este diagrama \(A=M_{f_{B_VB_W}}\) y \(C=M_{f_{B’_VB’_W}}\) es la matriz que desconocemos y buscamos. \(P=M_{B’_VB_V}\) es la matriz del cambio de base de \(B’_V\) a \(B_V\) y \(Q=M_{B’_WB_W}\). Así la matriz que buscamos es \[C=Q^{-1}\,A\,P.\]
Ejemplo
En el pasado ejercicio consideramos la aplicación lineal \(f:\mathbb{R}_2[X]\to\mathbb{R}_2[X]\) dada por \[\forall p(X)\in\mathbb{R}_2[X];\ f(p(X))=p(X)-\frac{d}{dX}p(X).\] Ahora buscamos su matriz asociada \(M_f\) respecto de la base \(B=\{1,1-X,1+X-X^2\}\). Si consideramos la misma aplicación sobre las bases canónicas, en este caso la misma al ser el mismo espacio vectorial, tendremos:
\[M_{fc}=\begin{bmatrix} f(1)\\ f(X)\\ f(X^2)\end{bmatrix}^t=\begin{bmatrix}1 & -1 & 0\\0 & 1 & -2\\ 0 & 0 & 1\end{bmatrix}\]
Del mismo modo,
\[M_{B}=\begin{bmatrix} 1\\ 1-X\\ 1+X-X^2\end{bmatrix}^t=\begin{bmatrix}1 & 1 & 1\\
0 & -1 & 1\\ 0 & 0 & -1\end{bmatrix}\]
Luego la matriz buscada es: \[M_{f_B}=M_{fc}M_B=\begin{bmatrix}1 & 2 & 0\\ 0 & -1 & 3\\ 0 & 0 & -1\end{bmatrix}.\]
Esto significa que si \((3,-2,5)\) son las coordenadas de un polinomio respecto de la base \(B=\{1,1-X,1+X-X^2\}\), cuando calculamos su imagen \(f(3,-2,5)=-5X^2+17X-1\) respecto de la base canónica, ya que \[\begin{bmatrix}1 & 2 & 0\\ 0 & -1 & 3\\ 0 & 0 & -1\end{bmatrix}\begin{bmatrix}3\\ -2\\ 5\end{bmatrix}=\begin{bmatrix}-1\\ 17\\ -5\end{bmatrix}.\]
Consideremos que queremos expresar la imagen respecto de una base \(B^\prime=\{1+2X,X-X^2,1+X^2\}\). Calculamos \[M_{B^\prime}=\begin{bmatrix} 1+2X\\ X-X^2\\ 1+X^2\end{bmatrix}^t=\begin{bmatrix}1 & 0 & 1\\ 2 & 1 & 0\\ 0 & -1 & 1\end{bmatrix}\]
Ahora la imagen respecto de esta base \(B^\prime\) será \[\begin{bmatrix}1 & 0 & 1\\
2 & 1 & 0\\ 0 & -1 & 1\end{bmatrix}^{-1}\begin{bmatrix}1 & 2 & 0\\ 0 & -1 & 3\\ 0 & 0 & -1\end{bmatrix}\begin{bmatrix}3\\ -2\\ 5\end{bmatrix}=\begin{bmatrix}13\\ -9\\ -14\end{bmatrix}\]
Supongamos que queremos saber qué polinomio, con coordenadas \((a,b,c)\) en la base \(B\), tiene por imagen \(f(a,b,c)=1\cdot(1+2X)+(-2)\cdot (X-X^2)+(-1)\cdot(1+X^2)\); es decir, tiene por coordenadas \((1,-2,-1)\) en la base \(B^\prime\). Entonces \[\begin{bmatrix}1 & 1 & 1\\
0 & -1 & 1\\ 0 & 0 & -1\end{bmatrix}^{-1} \begin{bmatrix}1 & 0 & 1\\
2 & 1 & 0\\ 0 & -1 & 1\end{bmatrix} \begin{bmatrix}1\\ -2\\ -1\end{bmatrix}=\begin{bmatrix}5 & -4 & 7\\ -2 & 2 & -3\\ 0 & 1 & -1\end{bmatrix}\begin{bmatrix}1\\ -2\\ -1\end{bmatrix}=\begin{bmatrix}6\\ -3\\ -1\end{bmatrix}\]
Como habitualmente tratamos los espacios vectoriales \(\mathbb{R}^n\) (recordad que todo espacio vectorial finitamente generado, de dimensión \(n\), es isomorfo a \(\mathbb{R}^n\)), este gráfico se representaría como
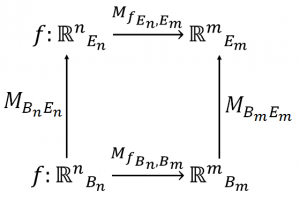
donde \(E_n\) y \(E_m\) son las bases canónicas respectivas.
|
Ejercicio: Sean los subespacios vectoriales \(S=\textbf{Gen}\{[[1,2],[2,1]],[[0,-1],[1,1]]\}\in\mathcal{M}_2(\mathbb{R})\) y \(T=\textbf{Gen}\{[[-1,0],[3,-1]],\)\([[1,9],[9,-2]],\)\([[3,10],[2,-1]]\}\in\mathcal{M}_2(\mathbb{R})\). ¿\(\textbf{dim}(S+T)\)? |