Sea \(f\) una función definida en un punto \(x_0\) de un intervalo \((a,b)\), denominaremos derivada de \(f\) en \(x_0\) al valor del límite, cuando exista,
\[\displaystyle\lim_{x\to x_0}\dfrac{f(x)-f(x_0)}{x-x_0}\]
En ese caso lo notaremos mediante \(f'(x_0)\).
Esta definición es equivalente a \[\displaystyle\lim_{h\to 0}\dfrac{f(x_0+h)-f(x_0)}{h}=f'(x_0),\] y más apropiada para definir la función derivada.
Llamamos función derivada de la función \(f\) en el intervalo \([a,b]\) a la función
\[f'(x)=\lim_{h\to 0}\dfrac{f(x+h)-f(x)}{h},\; \forall x\in[a,b]\]
cuando este existe.
Una función es derivable si existe su derivada en todos los puntos de su dominio. Recordemos que para esto debe existír y coincidir los límites laterales. Esto nos lleva a observar que una función puede ser continua en un punto, pero no derivable; por ejemplo, la función \(f(x)=|x|\) es continua en \(x=0\), pero no derivable. Sin embargo, toda función derivable es continua.
El paso siguientes es conocer las reglas de derivación para poder derivar cualquier función conocida. Recordemos que \(\forall \;\lambda,\mu\in\mathbb{R}\) es\[\begin{array}{rl}\textit{i)}& (\lambda f\pm \mu g)’ =\lambda f’\pm \mu g’ \\ \textit{ii)}&
(f\cdot g)’ =f’g+fg’, \\ \textit{iii)}& \left(\dfrac{f}{g}\right)’=\dfrac{f’g-fg’}{g^2}, \mbox{ si } g(x)\neq 0 \\
\end{array}\]
Podemos ver más propiedades de las funciones continuas en la bibliografía referenciada.
Regla de la cadena: Si \(h(x)=f(g(x))\) entonces \[h^\prime(x)=f(^\prime g(x))g\prime()\]
Ejemplo: Determinar el valor de \(f^\prime(1)\) donde \[f(x)=e^{\sin \left(x^2\right)}\]
Ejemplo: Determinar el valor de \(f^\prime(1)\) donde \[f(x)=\sin \left(x^2+\frac{1}{x}\right)\]
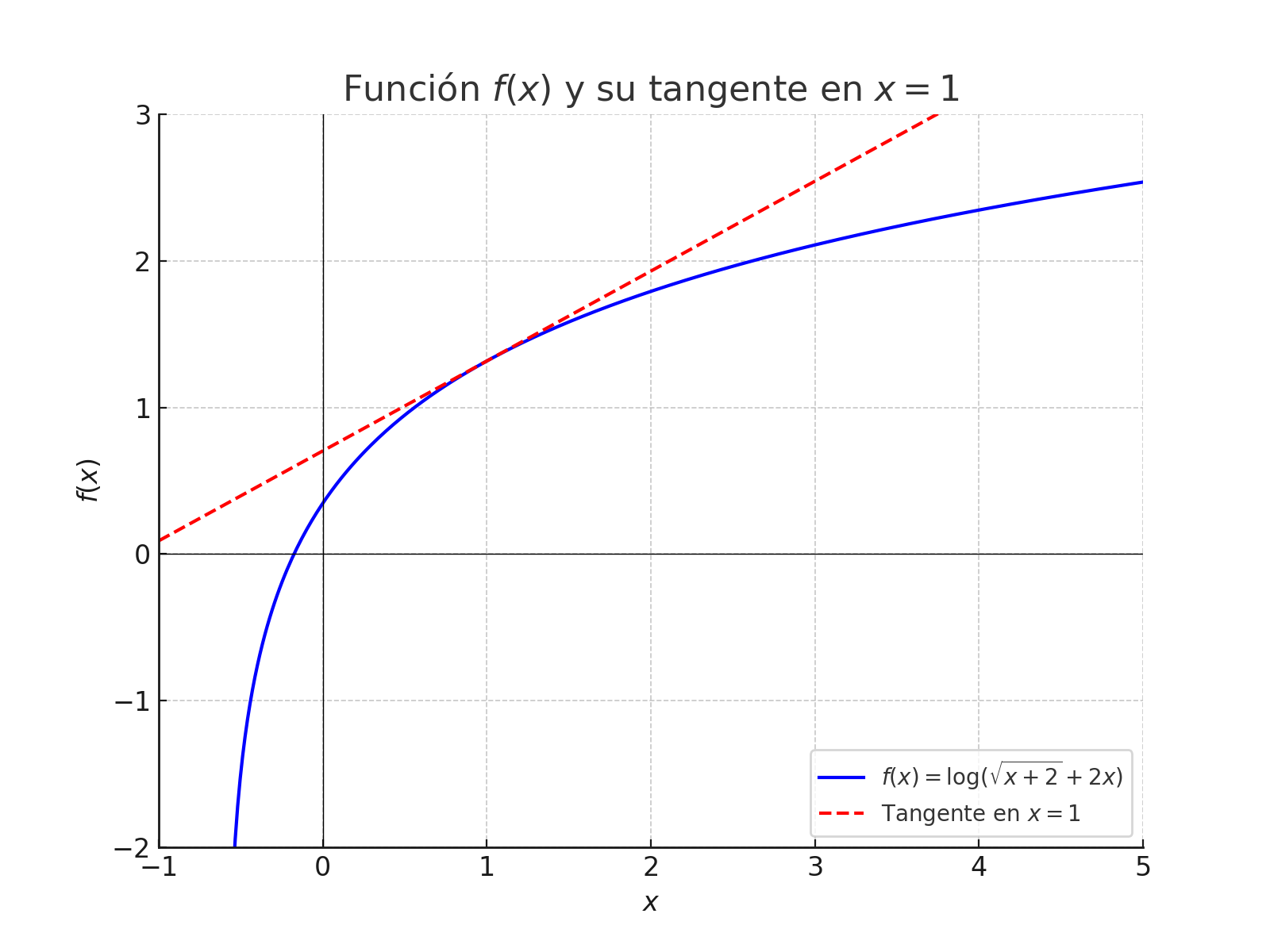
Ejemplo: Determinar el valor de \(f^\prime(1)\) donde \[f(x)=\log \left(\sqrt{x+2}+2x\right)\]
Recta tangente
Utilicemos esto para determinar la tangente a una función en un punto.
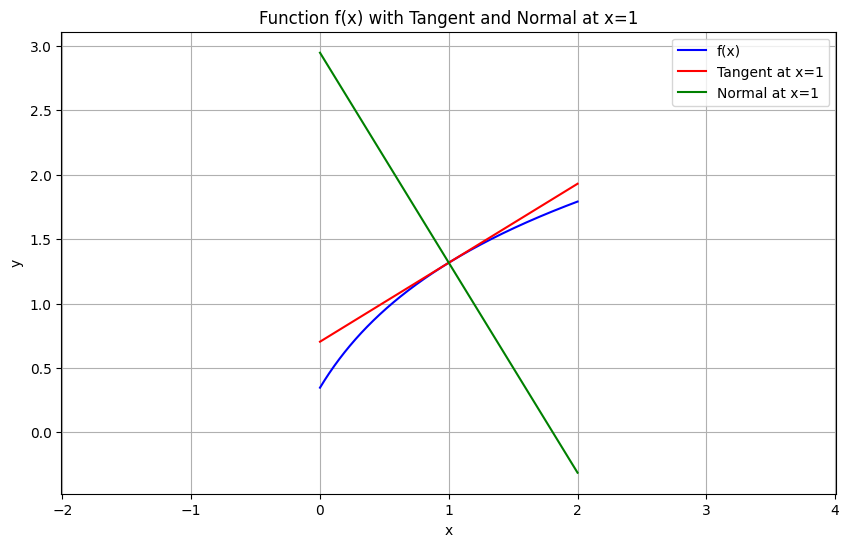
Ejemplo: Calcular la tangente a la función \(f(x)=\log \left(\sqrt{x+2}+2x\right)\), en \(x=1\)
Ejemplo: Sea \(T(x)\) la tangente a la función \(f(x)=x\ e^{-2x}+1\), en \(x=0\), ¿Cuál es el valor de \(T(0.2)\)
Recta normal
Si hemos planteado la derivada para encontrar la recta tangente, esta nos permite determinar la normal.
La recta tangente en un punto \(x_0\) a una curva \(y=f(x)\) vendrá dada por \[y-f(x_0)= f'(x_0)(x-x_0),\]
con lo cual, (\(-f'(x_0),1\)) es el vector director de la recta como subespacio vectorial en el plano real.
La normal es perpendicular a la recta tangente, por tanto \((1/f'(x_0),1)\) será su vector director, y la recta quedará definida mediante:
\[y-f(x_0)= \frac{-1}{f'(x_0)}(x-x_0).\]
Ejemplo: Calcular la normal a la función \(f(x)=\log \left(\sqrt{x+2}+2x\right)\), en \(x=1\)
Ejemplo: Sea \(N(x)\) la recta normal a la función \(f(x)=x\ e^{-2x}+1\), en \(x=0\), ¿Cuál es el valor de \(N(2)\)
Bibliografía
- Capítulo 3 del libro Biocalculus: Calculus for Life Sciences, de James Stewart.
|
Ejercicio: ¿Cuál es la recta tangente a la curva \(y=\frac{x^2-1}{x^2+x+1}\) en el punto (1,0)? |