MathBio: Sistemas, Autovalores y Funciones reales con maxima

Sistemas de ecuaciones

En pasados días vimos cómo resolvíamos sistemas de ecuaciones y, en particular, el problema de mínimos cuadrados mediante matrices. Hoy bordaremos estos problemas utilizando maxima.

linsolve($[eq_1, …, eq_m], [x_1, …, x_n]$): Solves the list of simultaneous linear equations for the list of variables. The expressions must each be polynomials in the variables and may be equations.

Ejemplo: Resolver el sistema de ecuaciones \[\begin{matrix}2x+y-z=1 \\x-3y+2z=1 \\ -x+2y-4z=2\end{matrix}\]

El sistema puede tener infinitas soluciones, en cuyo caso estas se dan en forma paramétrica:

Ejemplo: Resolver el sistema de ecuaciones \[\begin{matrix}3x-y-z+t=2 \\ x+y-2z-5t=1 \end{matrix}\]

En muchos casos los sistemas no tiene solución; si embargo, podremos optar por encontrar una solución por mínimos cuadrados.

Ejemplo: El pasado día vimos una tabla en base a la ley que nos dice que el volumen de un gas a presión constante crece de manera lineal con respecto a la temperatura. En los experimentos, a Jacques Charles la experimentación le proporcionó los siguientes datos:
\[\begin{array}{l|cccc}
T & -40 & -20 & 0 & \\ \hline
V & 19.1482 & 20.7908 & 22.4334 \\ \hline
T & 20 & 40& 60& 80 \\ \hline
V & 24.0760 & 25.7186 & 27.3612 & 29.0038 \\ \hline
\end{array}\] donde un mol de hidrógeno se mantiene a una presión constante de una atmósfera; siendo el volumen $V$ aproximado y medido en litros y la temperatura $T$ grados Celsius. Determinar una recta que relacione el volumen $V$ y la temperatura $T$ mediante una relación lineal.

Ejemplo: Encontrar la parábola que mejor se ajuste a los puntos [1,5.5],[-1,15.5],[3,11.2][-2,26.4]

Autovalores y autovectores

Recordemos que los vectores propios, eigenvectores o autovectores de una matriz son los vectores no nulos que, cuando son multiplicados por la matriz, dan lugar a un múltiplo escalar de sí mismos (con lo que no cambian su dirección). Este escalar ${\displaystyle \lambda }$ recibe el nombre valor propio, autovalor o valor característico.

Ejemplo: ¿Cuántos autovalores distintos tiene la matriz dada? \[\begin{bmatrix}1&0&0&1\\0&1&2&-1\\ 0&1&-1&0\\ 0&2&0&-1\end{bmatrix}\]

Ejemplo: ¿Cuál es la suma de las normas de los autovectores de la matriz anterior?

Funciones

Una función ordinaria es aquella que ha sido construida mediante cualquiera de los métodos define o := y que es invocada utilizando paréntesis.

Ejemplo: Determina la suma de los valores de la función $f(x)=x\,e^{1-x^2}$ para $x_i=\frac{i}{4}$ para $i\in\{1,\ldots,5\}$

(%i3)

f(x):=x*%e^(1–x^2)$
val:makelist(f(i/4),i,1,5);
sum(val[i],i,1,5),numer;

$\begin{matrix} (val) & [\frac{{%e}^{\frac{15}{16}}}{4}, \frac{{%e}^{\frac{3}{4}}}{2}, \frac{3 {%e}^{\frac{7}{16}}}{4}, 1, \frac{5 {%e}^{- \frac{9}{16}}}{4}] \end{matrix}$ $\begin{matrix} (%o3) & 4.570748627711323 \end{matrix}$

define($f(x_1,\ldots, x_n)$, expr): Define una función de nombre $f$ con argumentos $x_1,\ldots, x_n$ y cuerpo expr. define evalúa siempre su segundo argumento, a menos que se indique lo contrario con el operador de comilla simple.

Esta función la utilizaremos más adelante.

Gráfica de una función

wxplot2d(expresión, [variable,mínimo,máximo],opciones): La función wxplot2d representa uno o más gráficos en dos dimensiones. Las expresiones o nombres de funciones que se utilicen para definir curvas deben depender todas ellas de una única variable var, siendo obligatorio utilizar x_range para nombrar la variable y darle sus valores mínimo y máximo usando la siguiente sintaxis: [variable, min, max].

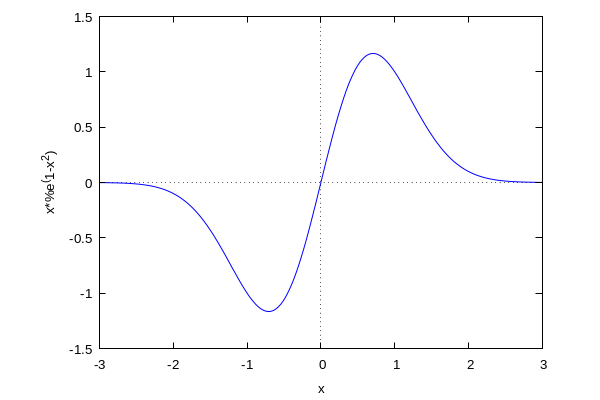
Ejemplo: Dibuja la función $f(x)=x\,e^{1-x^2}$ para $x\in[-3,3]$

(%i2)

f(x):=x*%e^(1–x^2)$
wxplot2d(f(x),[x,–3,3]);

$\begin{matrix} (%t2) \end{matrix}$ (Gráficos)
$\begin{matrix} (%o2) \end{matrix}$

Límites

Si queremos calcular un limite utilizaremos:

limit(expr)
limit(expr, x, val)
limit(expr, x, val, dir): Calcula el límite de expr cuando la variable real x se aproxima al valor val desde la dirección dir. El argumento dir puede ser el valor plus para un límite por la derecha, minus para un límite por la izquierda o simplemente se omite para indicar un límite en ambos sentidos.

Ejemplo: Calcular \[\lim_{x\to 0}\frac{3^x-3^{-x}}{3^x+3^{-x}}\]

(%i2)

f(x):=(3^x–3^(–x))/(3^x+3^(–x))$
limit(f(x),x,0);

$\begin{matrix} (%o2) & 0 \end{matrix}$

Ejemplo: Calcular \[\lim_{x\to \pm \infty}\frac{3^x-3^{-x}}{3^x+3^{-x}}\]

(%i2)

f(x):=(3^x–3^(–x))/(3^x+3^(–x))$
limit(f(x),x,inf);
limit(f(x),x,–inf);

$\begin{matrix} (%o2) & 1 \end{matrix}$ $\begin{matrix} (%o3) & - 1 \end{matrix}$

Ejemplo: Estudiar la continuidad de la función $f(x)=\frac{x-1}{\sqrt{x^2-3x+2}}$

(%i2)

f(x):=(x–1)/(sqrt(x^2–3*x+2))$
raiz:solve(x^2–3*x+2);

$\begin{matrix} (raiz) & [x = 1, x = 2] \end{matrix}$

(%i4)

limit(f(x),x,ev(x,raiz[1]),minus);
limit(f(x),x,ev(x,raiz[1]),plus);

$\begin{matrix} (%o3) & 0 \end{matrix}$ $\begin{matrix} (%o4) & 0 \end{matrix}$

(%i6)

limit(f(x),x,ev(x,raiz[2]),minus);
limit(f(x),x,ev(x,raiz[2]),plus);

$\begin{matrix} (%o5) & lim_{x \to 2 -} & \frac{x - 1}{\sqrt{x^{2} - 3 x + 2}} \end{matrix} \begin{matrix} (%o6) & \infty \end{matrix}$

Observar que la función no está definida para $x\in (1,2]$, de ahí que el límite cuando $x\to 2^-$ no se puede calcular.

Veamos si consideramos valores muy cercanos a $x=2$:

(%i8)

limit(f(x),x,1.999);
limit(f(x),x,2.001);

$\begin{matrix} (%o7) & - 31.60696125855515 %i \end{matrix}$ $\begin{matrix} (%o8) & 31.63858403911929 \end{matrix}$

Ejemplo: Estudiar la continuidad de la función $f(x)=\frac{x^2-4x-21}{x-7}$

(%i2)

f(x):=(x^2–4*x–21)/(x–7)$
limit(f(x),x,7,minus);
limit(f(x),x,7,plus);

$\begin{matrix} (%o2) & 10 \end{matrix}$ $\begin{matrix} (%o3) & 10 \end{matrix}$

(%i4)

solve(x^2–4*x–21,x);

$\begin{matrix} (%o4) & [x = - 3, x = 7] \end{matrix}$

(%i6)

rat(f(x));
ev(%,x=7);

$\begin{matrix} (%o5)/R/ & x + 3 \end{matrix}$ $\begin{matrix} (%o6)/R/ & 10 \end{matrix}$

Ejemplo: Calcular los límites de la función $f(x)=\frac{x^2+2x-1}{(x-1)e^x}$, en 0, $\pm \infty $ y los laterales en 1.

Propiedades de las funciones continuas

En muchos casos tendremos que buscar un cero de una función, aunque veremos métodos para encontrar las soluciones de una ecuación, vamos a trabajar con un resultado que nos ayudará a practicar más con maxima.

TeoremaSea $\displaystyle f:[a,b]\to \mathbb{R}$ una función real continua en $[a,b]$ con $f(a)<0<f(b)$ $c\in (a,b)$ tal que $f(c)=0$.

Este resultado nos proporciona el conocido método de bisección: dado un intervalo, es suficiente con verificar la diferencia de signo de la función entre los extremos y el punto medio, para determinar en qué subintervalo se encuentra la solución.

Ejemplo: Encontrar el cero de $f(x)=x^3+x^2-x-2$ con el método de bisección.

Ejercicio:Sea el sistema \[\begin{array}{l}2x-y-Kz=0 \\ x-y-2z=1 \\ -x+2z=K\end{array}\] El valor de $K$ que hace el sistema incompatibles divide a