En la presentación del día de hoy hemos visto
- Presentación
- Objetivos de la asignatura
- Metodología y Evaluación
- Bibliografía
Objetivos, Metodología y Evaluación
El contenido de la asignatura está centrado en tres bloques:
- Teoría de números
- Teoría de grafos
- Combinatoria y Lógica
Sea \(F_n=2^{2^n}+1\), ¿en qué cifra termina \(F_{12}\)?
Dado el mapa de Königsberg, con el río Pregel dividiendo el plano en cuatro regiones distintas, que están unidas a través de los siete puentes, ¿es posible dar un paseo comenzando desde cualquiera de estas regiones, pasando por todos los puentes, recorriendo solo una vez cada uno, y regresando al mismo punto de partida?
De Bogdan Giuşcă – Public domain (PD),based on the image, CC BY-SA 3.0, Enlace
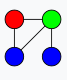
En Teoría de grafos, la coloración de grafos es un caso especial de etiquetado de grafos; es una asignación de etiquetas llamadas colores a elementos del grafo. De manera simple, una coloración de los vértices de un grafo tal que ningún vértice adyacente comparta el mismo color es llamado vértice coloración. Considera el grafo
¿Cuántas coloraciones diferentes puedes hacer?
En la guía de Grado podéis encontrar la metodología y la evaluación.
Inducción matemática
El ejercicio anterior lo hemos resuelto utilizando esta herramienta que nos será muy útil: la Inducción matemática, una herramienta tremendamente ágil para ciertos ejercicios que veremos,
La inducción matemática ayuda a demostrar una proposición determinada mediante el esquema del razonamiento siguiente. Llamemos \(P_n\) a la proposición, donde \(n\) es el rango.
- Se demuestra que \(P_0\), el primer valor que cumple la proposición (iniciación de la inducción), es cierta.
- Se demuestra que si se asume \(P_k\) como cierta y como hipótesis inductiva, entonces \(P_{k+1}\) lo es también, y esto sin condición sobre el entero natural \(k\) (relación de inducción).
Luego, demostrado esto, concluimos por inducción, que \(P_n\) es cierto para todo natural \(n\).
La inducción puede empezar por otro término que \(P_0\), digamos por \(P_{n_0}\). Entonces \(P_n\) será válido a partir del número \(n_0\), es decir, para todo natural \(n \ge n_0\).
Ejemplo: Para todo impar \(n\in\mathbb{Z}^+\), \(8\mid (n^2-1)\)
Bibliográfica
Básica
- García Merayo F., Matemática Discreta. Ed. Paraninfo, 2015
- García Merayo F., Hernández G., Nevot A. Problemas resueltos de Matemáticas Discreta., Ed. Paraninfo, 2018
Aconsejable
- Vieites A. M., y otros. Teoría de grafos. Ejercicios y problemas resueltos. Paraninfo, 2014.
- Lipschutz S., Lipson M. 2000 Problemas resueltos de matemática discreta. McGraw-Hill, 2004
- Bujalance, E. y otros. Elementos de Matemática Discreta. Ed. Sanz y Torres, Madrid, 2005
- Bujalance, E. y otros. Problemas de Matemática Discreta. Ed. Sanz y Torres, Madrid, 2005
- Grimaldi, R. P. Discrete and Combinatorial Mathematics. Pearson New International Edition, 2013