Abordemos cómo hacer la derivada a funciones reales de una variable real:
- diff(expr, variable, veces): Calcula la derivada de una Función que depende de la variable el número de veces indicado. El número veces puede eludirse si es uno. Si aparecen otras variables en expr son consideradas como constantes.
Cuando queremos utilizar la derivada como función si es conveniente usar define:
- define(\(f(x_1,\ldots, x_n)\), expr): Define una función de nombre \(f\) con argumentos \(x_1,\ldots, x_n\) y cuerpo expr. define evalúa siempre su segundo argumento, a menos que se indique lo contrario con el operador de comilla simple.
Ejemplo: Determinar el valor de \(f^\prime(1)\) donde \[f(x)=e^{\sin \left(x^2\right)}\]
Ejemplo: Determinar el valor de \(f^\prime(1)\) donde \[f(x)=\sin \left(x^2+\frac{1}{x}\right)\]
Ejemplo: Sea \(T(x)\) la recta tangente a \(y=x^2\sin(x/2)\) en \(x=\pi/3\), calcula \(T(5)\)
Ejemplo: Sea \(N(x)\) la recta normal a \(y=\frac{-{{x}^{2}}-11 }{2 {{x}^{3}}}\) en \(x=-2\), calcula \(N(5)\)
Concavidad y convexidad de una función
Veamos cómo utilizamos la derivada para estimar la concavidad o convexidad de una función. En este caso utilizaremos también otra herramienta para gráficos:
- draw2d(): capaz de gestionar, uno o varios gráficos simultáneamente, que pueden ser de tipos diferentes (fórmulas en explícitas, en implícitas, en paramétricas, en polares…) cada uno con sus propios parámetros y opciones (que se precisan antes de declarar la figura); también existen opciones globales que afectan a todos los elementos (por ejemplo, el título del conjunto) y que es conveniente (pero no imprescindible) colocar al principio
Ejemplo: ¿Cuál es el módulo del vector formado por del punto (1,1) y el punto la parábola \(y^2=2x\) más cercano a el?
Ejemplo: En qué intervalo la función \(f(x)=x\,e^{1-x^2}\) es cóncava
Método de Newton
Como hemos observado necesitamos conocer las soluciones de las ecuaciones que plantean las funciones para encontrar máximos y mínimos o los cambios de concavidad y convexidad. Repasemos el método de bisección para encontrar un cero, y apliquemos un método más preciso:El Método de Newton.
Ejemplo: Encontrar los ceros de la segunda derivada de \(f(x)=x\,e^{1-x^2}\) con el método de bisección.
Método de Newton Sea \( f:[a,b]\to \mathbb {R}\) una función derivable definida en el intervalo real \([a,b]\) y \(x_p\in [a,b]\) tal que \(f(x_p)=0\). Entonces para cierto \(x_{0}\in [a,b]\) la sucesión \[x_{{n+1}}=x_{n}-{\frac{f(x_{n})}{f^\prime(x_{n})}},\]
cumple que \(\lim_{n\to\infty}x_n=x_p\).
Ejemplo: Encontrar el cero de \(f(x)=x^3-x^2+2x+1\)
Ejemplo: Sea \(s\) la abscisa donde las curvas \(y=x^2-x\) e \(y=\sqrt{x}\) se cortan en el intervalo [1,2], ¿cuál es la parte entera del valor de \(e^s+e^{s+1}\)?
Funciones de varias variables
El siguiente comando nos permitirá realizar la gráfica de un campo escalar.
- plot3d(expresión, [variable_x mínimo, máximo], [variable_y mínimo, máximo], opciones):
La expresión es del tipo f(x,y) y corresponde a z=f(x,y) para coordenadas cartesianas
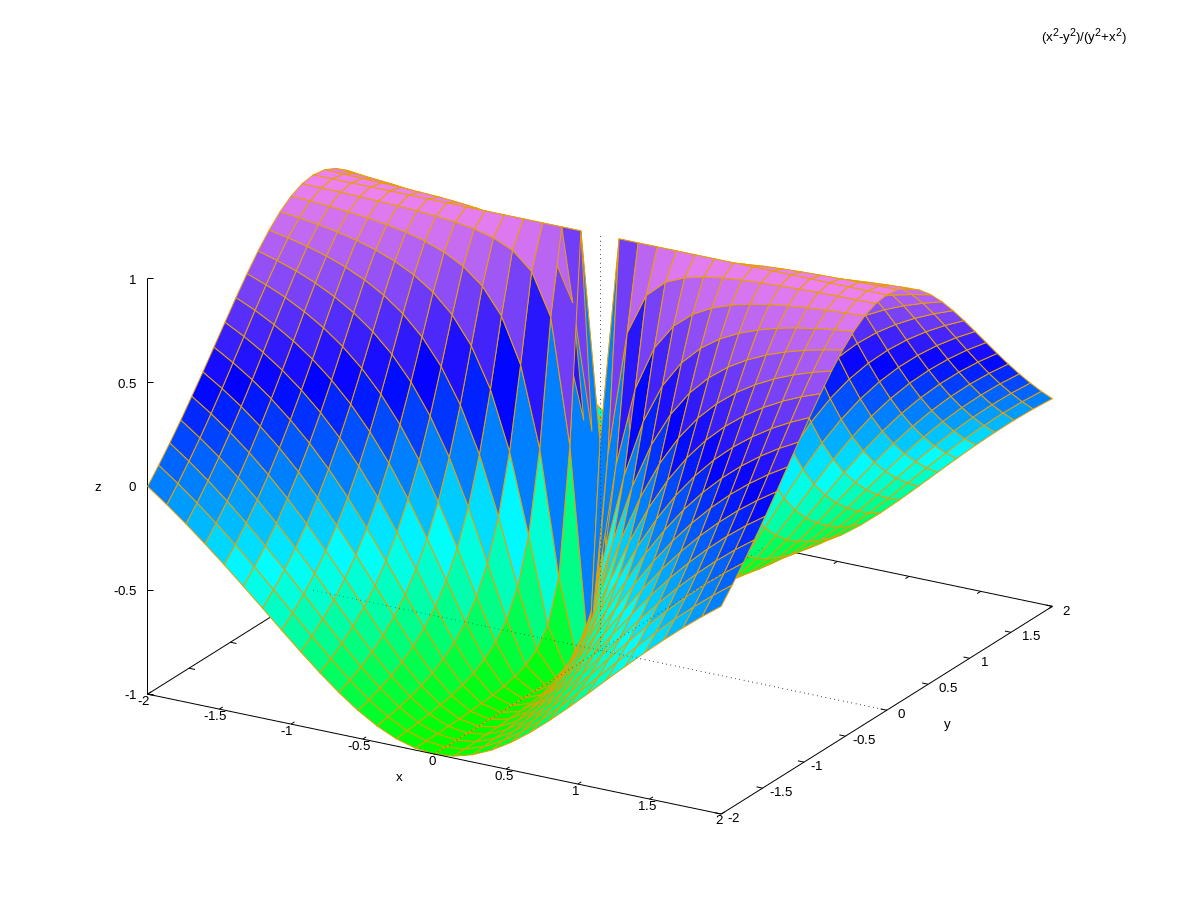
Ejemplo: Dibujar la gráfica de \(f(x,y)=(x^2-y^2)/(x^2+y^2)\) en [-2,2]x[-2,2].
Ejemplo: Sea \(f(x,y)=\frac{x}{(x+y)^2}\). ¿Cuánto vale \(f_x(1,1)+f_y(1,1)\)?
Ejercicio: Sea \(f(x,y)=\frac{x}{(x+y)^2}\). ¿Cuánto vale \(\frac{dy}{dx}(1,0)\)?
Ejercicio: Determinar la ecuación de la recta tangente a la curva \(xy-y^2-2y^3=0\), en el punto (1,-1)
Ejemplo: Determinar el vector gradiente de \(f(x,y,z)=x\,\sin^2(y)+z\,\cos^2(y)\)
Ejemplo: Sea \(f(x,y,z)=x\,\sin^2(y)+ze^{2x}\). ¿Cuánto vale \(\left \|\nabla f\left(1,\tfrac{\pi}{4},0\right) \right \|\) ?
Ejemplo: calcular la derivada direccional de \(f(x,y,z)=x\,\sin(y)+yz^2\) en el punto P(1,\(\frac{\pi}{2}\),-1) y en la dirección del vector u=(4,3,0).
| Ejercicio:Sea \(f(x,y,z)=\cos^2(x)+ze^{-y}\). ¿Cuánto vale \(\left \|\nabla f\left(\pi,-1,1\right) \right \|\) ? |