MathBio: Aplicaciones de las derivadas parciales

Hoy vamos a ver aplicaciones importantes de las derivadas parciales:

Derivación implícita.

Derivación implícita

Consideremos una ecuación que define a \(y\) en forma implícita; es decir, \(F(x, y)=0\) es una función implícita en cierta región de \(\mathbb{R}^2\) entre las variables \(x\) e \(y\), es fácilmente derivable utilizando la derivación implícita: \[\frac{\partial F}{\partial x}\frac{dx}{dx}+\frac{\partial F}{\partial y}\frac{dy}{dx}=0,\] si \(\frac{\partial F}{\partial y}\neq 0\), tendremos \[\frac{dy}{dx}=-\frac{\partial_x F}{\partial_y F },\]
con siempre que \(\partial_y F\neq 0\).

Ejemplo: Sea \(x^2-xy+2y^3=0\), ¿cuál es el valor de \(y^\prime(x_0)\) en (1,-1)?

Ejemplo: Sea \(f(x,y)=\frac{x}{(x+y)^2}\). ¿Cuánto vale \(\frac{dy}{dx}(1,0)\)?

En el caso \(F(x, y, f(x, y)) = 0\) si \(z = f(x, y)\) define una función implícita para \(z\) en términos de \(x\), \(y\) entonces podemos calcular sus derivadas parciales de la siguiente manera, usando la regla de la cadena
\[\frac{\partial F}{\partial x }\ \frac{\partial x}{\partial x }+
\frac{\partial F}{\partial y }\ \frac{\partial y}{\partial x }+
\frac{\partial F}{\partial z }\ \frac{\partial z}{\partial x }=0\Rightarrow \]
\[\frac{\partial F}{\partial x }\ \frac{\partial x}{\partial x }+
\frac{\partial F}{\partial z }\ \frac{\partial z}{\partial x }=0\]
ya que \(\frac{\partial y}{\partial x }=0\). Luego
\[\frac{\partial z}{\partial x }= -\frac{\partial_x F}{\partial_z F },\]
siempre que \(\partial_z F\neq 0\).

Ejemplo: Sea \(f(x,y,z)=x^2+y^2+z^2-3\), ¿cuál es el valor de \(\frac{\partial z}{\partial y}(1,1,1)\) ?

Recta tangente a una curva en \(\mathbb {R} ^{2}\)

Atendiendo lo que hemos visto anteriormente, si \(F(x,y)=0\) representa una curva diferenciable en \(\mathbb {R} ^{2}\), la recta tangente en un punto \((x_0,y_0)\in\mathbb {R} ^{2}\) de la curva, vendrá dada por
\[[\partial_xF(x_0,y_0)\ \partial_yF(x_0,y_0)]\begin{bmatrix} x-x_0\\ y-y_0 \end{bmatrix}=0\]
que es lo mismo que \[ \left ( y-y_0 \right )=-\left ( \frac{{\partial_x F(x_0,y_0)}}{\partial_y F(x_0,y_0)} \right )\left ( x-x_0 \right ).\]

Ejemplo: Determinar la ecuación de la recta tangente a la curva \(xy-y^2-2y^3=0\), en el punto (1,-1)

Observar que si \(y=f(x)\); es decir \(F(x,y)=F(x,f(x))=0\), es una función explícita, entonces la expresión anterior es la misma que la conocida \[ \left ( y-y_0 \right )=-\left ( \frac{{d f}}{dx}(x_0) \right )\left ( x-x_0 \right ).\]

Ejemplo: Sea \(\mathbf{T}(x)\) la recta tangente a \(x^{1/2} +y^{1/2} = 4\) en (4, 4), ¿cuánto es \(\mathbf{T}(-1)\)?

Ejemplo: Sea \(\mathbf{T}(x)\) la recta tangente a \(x^2 +3xy+y^2 = 5\) en (1, 1), ¿cuánto es \(\mathbf{T}(-1)\)?

Ejemplo: Cuántos puntos de la curva \(x^2y^2+xy=2\) cumplen que la pendiente de la recta tangente es -1.

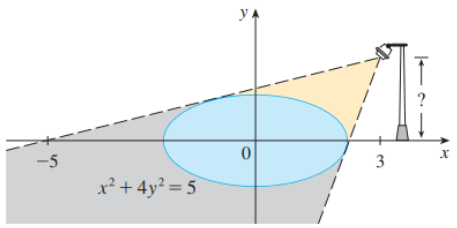
Ejemplo: En la figura se muestra una lámpara colocada tres unidades hacia la derecha del eje \(y\) y una sombra creada por la región elíptica \(x^2+4y^2\leq 5\). Si el punto (-5, 0) está en el borde de la sombra, ¿qué tan arriba del eje \(x\) está colocada la lámpara?