Veamos un ejemplo que utilizaremos con frecuencia de espacio vectorial, el de las matrices, donde veremos:
- Definición
- Matriz columna, matriz fila
- Matriz: traspuesta, identidad, cuadrada, triángular…
- Operaciones con matrices
- Suma de matrices
- Multiplicación de escalar por matriz.
- Semejanza de matrices
- matriz escalonada
- rango de una matriz
Lo primero será definir las matrices. Llamamos matriz fila a una disposición de \(p\) escalares de un cuerpo colocado en una fila por \(p\) columnas, \(A_f=[a_1\,a_2\,\ldots\,a_p]\), y del mismo modo definimos matriz columna disponiendo los \(p\) escalares sobre un columna: \(B_c=\begin{bmatrix}b_1\\ b_2 \\ \vdots \\ b_p\end{bmatrix}\).
De esta forma una matriz de \(n\times m\) a una disposición de \(n\) matrices fila o \(m\) matrices columna;
\[\begin{bmatrix}
a_{11} & a_{12} & a_{13} &\ldots & a_{1m} \\
a_{21} & a_{22} & a_{23} &\ldots & a_{2m} \\
\vdots & \vdots & \vdots &\ldots & \vdots \\
a_{n1} & a_{n2} & a_{n3} &\ldots & a_{nm}
\end{bmatrix}.\]
Notar que los elementos \(a_{ij}\in\mathbb{K}\), siendo \(\mathbb{K}\) un cuerpo, que habitualmente será los reales o los complejos.
Ejercicio: Sea \(A\)=[[x+2,8,-3],[1,2y,2x],[7,-2,y+2]] y \(B\)=[[2x+6,8,-3],[1,18,-8],[7,-2,11]], tales que \(A=B\). ¿Cuál es la suma de \(x+y\)?
Matrices particulares
Tenemos diferentes matrices que por sus características se les denomina de forma especial:
Matriz cuadrada: diremos que \(A=[a_{ij}]\) es cuadrada si \(i=1,\ldots,n\) y \(j=1,\ldots,n\)
Matriz identidad de orden \(n\) \[I_2= \begin{bmatrix}
1 & 0\\
0 & 1\\
\end{bmatrix}, I_3=\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix},\ldots\]
Matriz diagonal: una matriz donde todos los valores que no estén en la diagonal principal son cero, \[\begin{bmatrix}
a_1 & 0 & 0 &\cdots&0\\
0 & a_2 & 0 &\cdots&0\\
0 & 0 & a_3 &\cdots&0\\
\vdots&\vdots&\vdots&\cdots&0\\
0&0&0&\cdots&a_n
\end{bmatrix}\]
Matriz traspuesta: diremos que \(A^t\) es la matriz traspuesta de \(A=[a_{ij}]\) si \(A^t=[a_{ji}]\)
Matriz simétrica: diremos que \(A\) es simétrica si \(A=A^t\)
Matriz antisimétrica: Una matriz antisimétrica es una matriz cuadrada \(A\) cuya traspuesta es igual a su opuesta, es decir vale la relación \(A^t=-A\)
Matriz triangular: una matriz triangular es un tipo especial de matriz cuadrada cuyos elementos están por encima o por debajo de su diagonal principal o su diagonal secundaria son cero.
Una matriz cuadrada de orden n se dice que es triangular superior si es de la forma: \[{\displaystyle U=\left[{\begin{array}{ccccccc}u_{11}&u_{12}&u_{13}&.&.&.&u_{1n}\\0&u_{22}&u_{23}&.&.&.&u_{2n}\\0&0&u_{33}&.&.&.&u_{3n}\\.&.&..&.&.&.&.\\.&.&.&.&.&.&.\\.&.&.&.&.&.&.\\0&0&0&.&.&.&u_{nn}\\\end{array}}\right]}\]
Análogamente, se dice que es una matriz triangular inferior una matriz de la forma: \[{\displaystyle L=\left[{\begin{array}{ccccccc}l_{11}&0&0&.&.&.&0\\l_{21}&l_{22}&0&.&.&.&0\\l_{31}&l_{32}&l_{33}&.&.&.&0\\.&.&.&.&.&.&.\\.&.&.&.&.&.&.\\.&.&.&.&.&.&.\\l_{n1}&l_{n2}&l_{n3}&.&.&.&l_{nn}\\\end{array}}\right]}\]
Operaciones con matrices
Ahora podemos definir la suma de matrices,\(A=[a_{ij}]_{nxm}\) y \(B=[b_{ij}]_{n\times m}\), como otra matriz de la siguiente forma:
\[A+B=[a_{ij}+b_{ij}]_{n\times m}.\]
Y el producto por escalar, \(\lambda\in \mathbb{K}\), de la forma:
\[\lambda A=[\lambda a_{ij}]_{n\times m}.\]
Con estas operaciones se cumple: Consideremos \(\lambda,\mu\in \mathbb{K}\) y \(A,B,C\in M_{n\times m}(\mathbb{K})\), siendo \(\mathbb{K}\) el conjunto de los números reales o complejos,
- \((A+B)+C=A+(B+C)\)
- \(A+B=B+A\)
- \(A+0=0+A\), siendo 0 la matriz de \(m\times n\) elementos todos 0.
- Existe \(B\in M_{m\times m}(\mathbb{K})\) tal que \(A+B=B+A=0\), a esta matriz la llamamos opuesta de \(A\), que designamos por \(-A\).
- \(\lambda (A+B)=\lambda A+\lambda B\)
- \((\lambda + \mu)A=\lambda A+\mu A\)
- \((\lambda \mu)A=\lambda (\mu A)\)
Ejercicio: Sea \(A\)=[[4,-1,6],[2,1,6],[2,-1,8]] y \(B\)=[[0,-1,5],[1,6,2],[1,8,0]]. ¿Cuál es la suma de los elementos de la diagonal principal de \(2A-3B\)?
Ejercicio: Sea \(A\)=[[4,-1,6],[2,1,6],[2,-1,8]] y \(B\)=[[0,-1,5],[1,6,2],[1,8,0]]. ¿Cuál es el valor de \(\lambda\) para que la suma de los elementos de la diagonal principal de \(\lambda A-3B\) sea -18?
Ejercicio: Dadas las matrices \(A=\begin{bmatrix}1&-1\\ 2&3\end{bmatrix}\) y \(B=\begin{bmatrix}-1&0\\ 2&3\end{bmatrix}\). ¿Cuál es la matriz \(X\) que cumple \(3(2A+B+X)=5(X-A+B)\)?
Lo siguiente que hemos visto es la Multiplicación de matrices:
Definimos el producto de una matriz fila \(A_f\) por una matriz columna \(B_c\), siempre que el número de columnas de la matriz fila coincida con el número de filas de la matriz columna, como el producto escalar considerándolos vectores la matriz fila \(A_f\) y la traspuesta de \(B_c\):
\[A_f\cdot B_c=[a_1\,a_2\,\ldots\,a_p]\bullet \begin{bmatrix}b_1\\ b_2 \\ \vdots \\ b_p\end{bmatrix}=(a_1\,a_2\,\ldots\,a_p)\cdot \begin{pmatrix}b_1\\ b_2 \\ \vdots \\ b_p\end{pmatrix}^t=a_1b_1+a_2b_2+\ldots +a_pb_p.\]
De este modo el producto de dos matrices \(A=[a_{ij}]_{n\times p}\) y \(B=[b_{ij}]_{p\times m}\) es la matriz \[C=[A_i\bullet B_j]_{n\times m},\]
donde \(A_i\) es la fila \(i\) de la matriz \(A\) y \(B_j\) la columna \(j\) de la matriz \(B\). Esta forma de definir el producto es equivalente a la denotada por \(A\cdot B,\;A\times B,\;A\circ B\) o simplemente \(AB\), la matriz \(C\):
\[C=AB=[c_{ij}]_{n\times m}=\left[\sum _{p=1}^{n}a_{ip}b_{pj}\right]\]
Ejercicio: Sea \[\begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix}\begin{bmatrix} a & b\\ c & d \end{bmatrix}=\begin{bmatrix} 6 & 3\\ 19 & 2 \end{bmatrix},\] ¿cuál es el valor de \(a^2+b^2+c^2+d^2\)?
Ejercicio: Sea \(A=\begin{bmatrix} 1 & 3\\ \alpha & 1 \end{bmatrix}\), ¿cuál es el valor de \(\alpha\) para el cual A es una raíz del polinomio \(f(x)=x^2-2x-8\)?
Ejercicio: Sea \(A\)=[[1,1],[0,1]]. ¿Cuál es la suma de los elementos de la primera fila de \(A^p\)?
Ejercicio: Sea \(A\)=[[4,5,-1],[-3,-4,1],[-3,-4,0]]. ¿Cuál es la suma de los elementos de la diagonal principal de \(A^9\)?
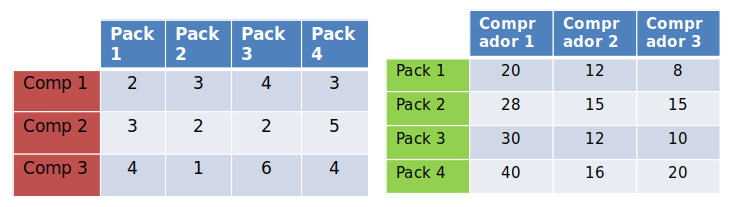
Ejercicio: Una empresa vende cuatro Pack que suministran tres tipos diferentes de componentes, dados en la Tabla 2. Tres compradores deciden comprar Pack, el número de Packs que compra cada uno está dado por la Tabla 1. ¿Cuántos componentes del nº2 compra el comprador nº3?
Tabla 1 Tabla 2
Propiedades que cumple la multiplicación de matrices:
- \((AB)C = A(BC)\)
- \((A + B)C = AC + BC\)
- \(C(A + B) = CA + CB\)
- Si A es una matriz cuadrada de tamaño \(m\), entonces la matriz identidad \(I_{m\times m}\) (que llamamos identidad, o elemento neutro para la multiplicación) de manera que: \(I·A = A·I = A\)
- El producto de dos matrices generalmente no es conmutativo, es decir, \(AB \neq BA\).
Ejercicio: Sea \(A\)=[[1,5],[-1,3],[2,1]], \(B\)=[[-1,4],[-2,5]], y \(C=(A.B)^t\)?
Semejanza por operaciones elementales en matrices y rango de una matriz
Consideremos \(A=[a_{ij}]\in \mathcal{M}_{m\times n}(\mathbb{R})\) una matriz y \(A(f_i)=[a_{i1}\ldots a_{in}]\) (respectivamente \(A(c_i)=[a_{1i}\ldots a_{mi}]’\)) una de las filas (respectivamente columnas) de la matriz.
LLamaremos operación elemental a una fila a las siguientes operaciones:
- \(f_i\leftarrow f_i+\lambda f_j\), proporciona una nueva matriz,\(B\), cuya fila \(B(f_i)=[b_{i1}\ldots b_{in}]\) cumple \(b_{ik}=a_{ik}+\lambda a_{jk}\) para \(k=1,\ldots,n\)
- \(f_i\leftarrow \lambda f_i\), proporciona una nueva matriz,\(B\), cuya fila \(B(f_i)=[b_{i1}\ldots b_{in}]\) cumple \(b_{ik}=\lambda a_{ik}\) para \(k=1,\ldots,n\)
- \(f_i\leftrightarrow f_j\), proporciona una nueva matriz,\(B\), cuyas filas \(B(f_i)=[b_{i1}\ldots b_{in}]\) y \(B(f_j)=[b_{j1}\ldots b_{jn}]\) cumplen \(b_{ik}=a_{jk}\) y \(b_{jk}=a_{ik}\) para \(k=1,\ldots,n\)
LLamaremos operación elemental a una columna a las siguientes operaciones:
- \(c_i\leftarrow c_i+\lambda c_j\), proporciona una nueva matriz,\(B\), cuya columna \(B(c_i)=[b_{1i}\ldots b_{mi}]’\) cumple \(b_{ki}=a_{ki}+\lambda a_{kj}\) para \(k=1,\ldots,m\)
- \(c_i\leftarrow \lambda c_i\), proporciona una nueva matriz,\(B\), cuya columna \(B(c_i)=[b_{1i}\ldots b_{mi}]’\), cumple \(b_{ik}=\lambda a_{ik}\) para \(k=1,\ldots,n\)(\(b_{ki}=\lambda a_{kj},k=1,\ldots,m\))
- \(c_i\leftrightarrow c_j\), proporciona una nueva matriz,\(B\), cuyas columnas \(B(c_i)=[b_{1i}\ldots b_{mi}]’\) y \(B(c_j)=[b_{1j}\ldots b_{mj}]’\), cumplen \(b_{ki}=a_{kj}\) y \(b_{kj}=a_{ki}\) para \(k=1,\ldots,m\)
En el siguiente polimedia tenéis esta explicación:
Definición: Dos matrices \(A\) y \(B\) son semejantes por transformaciones elementales, \(A\sim B\), si dada podemos obtener la otra mediante transformaciones elementales.
Decimos que una matriz es escalonada, cuando dado una matriz podemos encontrar una matriz semejante por transformaciones elementales que tiene en alguna de sus filas (columnas) todo los elementos cero. La matriz resultante escalonada será la matriz escalonada con mayor número de filas (columnas) todo cero que podamos conseguir.
En el siguiente polimedia tenéis esta explicación:
Propiedad: Toda matriz \(A\) es semejante por transformaciones elementales a una matriz escalonada: \(A\sim E\), donde \(E\) es escalonada.
Con estas definiciones podemos dar el rango de una matriz como el número de filas (columnas) distintas de cero de su matriz escalonada.
Una propiedad interesante es que el rango de una matriz siempre es el mismo, independientemente que se consideren filas o columnas.
Ejercicio: ¿Cuál es el rango de la matriz \(A=\begin{bmatrix}a&a&1&1\\ 1&a&a&1\\ 1&1&a&a\\ a&1&1&a\end{bmatrix}\) dependiendo del valor de \(a\)?
Propiedad: Dado un conjunto de vectores \(v_1,v_2,\ldots,v_m\in\mathbb{R}^n\), el número de vectores linealmente independientes es igual al rango de la matriz cuyas filas forman los vectores dados, \(rang[v_1,v_2,\ldots,v_m]\in\mathcal{M}_{n,m}(\mathbb{R})\).
Esta propiedad nos ofrece un método muy sencillo para determinar un subconjunto de vectores linealmente independiente.
Como corolario podemos ver que: Dado un conjunto de vectores \(v_1,v_2,\ldots,v_m\in\mathbb{R}^n\)
- \(rang[v_1,v_2,\ldots,v_m]\leq \mbox{min}\{n,m\}\)
- Si \(n< m\), serán linealmente dependientes.
- Si \([v_1,v_2,\ldots,v_m]\sim A\), donde \(A\) es una matriz escalonada, entonces los vectores linealemente independientes se corresponden con las filas no nulas de la matriz \(A\). Por el contrario, los linealemente dependientes se corresponden con las filas nulas de la matriz \(A\).
Ejercicio: Consideremos \(S=\mbox{Gen}\{(2,1,3),(-1,0,1)\}\), ¿(2,0,-1)\(\in S\)?
Ejercicio: Determinar si el punto \(S(1,2,-1)\) es coplanario a los puntos \(P(2,1,3)\),\(Q(-1,0,1)\) y \(R(2,0,-1)\).
Bibliografía
- Capítulo 2 de Álgebra lineal y sus aplicaciones. 5º edición, David C. Lay. Pearson. 2016.
| Ejercicio: Dadas la matrices \(A=\begin{bmatrix}2&2\\ 8&-2\end{bmatrix}\) y \(B=\begin{bmatrix}2&-2\\ 4&-2\end{bmatrix}\), la igualdad \(A^2+B^2=(A+B)^2\) es: |