ALG: Aplicaciones y matrices ortogonales

Aplicaciones y matrices ortogonales

Definimos las aplicaciones ortogonales a las aplicaciones de un espacio vectorial con producto escalar \((\mathcal{E},\bullet)\) que conservan el producto escalar; es decir, \(f:\mathcal{E}\to \mathcal{E}\), es ortogonal si \[f(\vec{x})\bullet f(\vec{y})=\vec{x}\bullet \vec{y},\quad\forall\,\vec{x}, \vec{y}\in\mathcal{E}\]

Propiedades que cumple una aplicación ortogonal:

• Es lineal
• Conserva la norma; es decir, \(||f(\vec{x})||=||\vec{x}||\)
• Dos vectores son ortogonales si, y solo si, sus imágenes son ortogonales
• La aplicación es biyectiva
• Los vectores propios de valores propios distintos son ortogonales
• La imagen de una base ortonormal es ortonormal
• Su matriz asociada es ortogonal

Hay varias formas de definir una matriz ortogonal. Nosotros emplearemos la que parte de la teoría de matrices.

Definición: Diremos que de una matriz cuadrada es ortogonal si su inversa coincide con su traspuesta; es decir,\[A^{-1}=A^t.\]

Ejercicio: ¿La matriz es \(\frac{1}{2}\begin{bmatrix}\sqrt{3}&1\\ -1&\sqrt{3}\end{bmatrix}\) es ortogonal?

Ejercicio: ¿La matriz es \(\frac{1}{5}\begin{bmatrix}4&0&-3\\ 0&5&0\\ 3&0&4\end{bmatrix}\) es ortogonal?

Ejercicio: ¿La matriz es \(\begin{bmatrix}1&2&0\\ 2&1&0\\ 0&0&-1\end{bmatrix}\) es ortogonal?

Ejercicio: ¿La matriz es \(\begin{bmatrix}0&0&1\\ 0&-1&0\\ -1&0&0\end{bmatrix}\) es ortogonal?

Ejemplo: ¿La matriz es \(\frac{1}{2}\begin{bmatrix}2&1&-2\\ 1&2&2\\ -2&2&-1\end{bmatrix}\) es ortogonal?

Solución:

Ejemplo: ¿Para qué valores de \(\alpha\) y \(\beta\), reales, la matriz \(\begin{bmatrix}0&\alpha&\beta\\ \alpha&\beta&0\\ \beta&0&\alpha\end{bmatrix}\) es ortogonal?

Solución:

Propiedad: Una matriz \(A\in\mathcal{M}_n(\mathbb{R})\) ortogonal, entonces \(\det(A)=\pm 1\).

En efecto, basta con observar que \[{\displaystyle \det(A\cdot A^{t})=\det A\ \det A^{t}=\det A\ \det A=(\det A)^{2}=\det I=1.}\]

Propiedad: Una matriz \(A\in\mathcal{M}_n(\mathbb{R})\) ortogonal, para todo \(\mathbf{u},\mathbf{v}\in\mathbb{R}^n\) es \(A\mathbf{u}\bullet A\mathbf{v}=\mathbf{u}\bullet \mathbf{v}\) y \(\|A\mathbf{u}\|=\|\mathbf{u}\|\).

Observemos que dados \(\mathbf{u},\mathbf{v}\in\mathbb{R}^n\), \[A\mathbf{u}\bullet A\mathbf{v}=\left( A\mathbf{u}\right) ^{t}\left( A\mathbf{v}\right) =\left( \mathbf{u}^{t}A^{t}\right) A\mathbf{v}=\mathbf{u}^{t}\left( A^{t}A\right) \mathbf{v}=\mathbf{u}^{t}\;I_{n}\;\mathbf{v}=\mathbf{u}^{t}\;\mathbf{v}=\mathbf{u}\bullet \mathbf{v}.\]
De aquí, vemos que \[\|A\mathbf{u}\|=\sqrt{A\mathbf{u}\bullet A\mathbf{u}}=\sqrt{\mathbf{u}\bullet \mathbf{u}}=\|\mathbf{u}\|\]

Para nosotros será muy útil el siguiente resultado:

Teorema: Una matriz \(A\in\mathcal{M}_n(\mathbb{R})\) es ortogonal si y sólo si sus vectores filas o vectores columna son cada uno un conjunto ortonormal de vectores.

Propiedad: Si \(A,B\in\mathcal{M}_n(\mathbb{R})\) son ortogonales, entonces el producto \(AB\) es ortogonal.

La relación entre los concepto de aplicación ortogonal y matriz ortogonal es muy sencilla:

Teorema: Si tenemos un endomorfismo ortogonal sobre una base ortonormal, entonces su matriz asociada es una matriz ortogonal.

Dicho de otro modo, las aplicaciones ortogonales, aquellas que conservan el producto escalar, tienen por matrices asociadas a matrices ortogonales (matrices cuadradas que cumplen que su inversa coincide con la traspuesta). Además se cumple, que en una matriz ortogonal las filas o columnas, consideradas como vectores, son ortonormales.

Clasificación de las aplicaciones ortogonales en \(\mathbb{R}^2\)

Teorema: Si \(f:\mathbb{R}^2\to\mathbb{R}^2\) es un endomorfismo ortogonal respecto una base ortonormal, entonces su matriz asociada es \[A=\begin{bmatrix}a& -b|A|\\ b& a|A|\end{bmatrix},\] con \(|A|=\pm 1\).

Giros

Si resulta \(|A|=1\), será \[A=\begin{bmatrix}a& -b\\ b& a\end{bmatrix}.\]
De este modo, exíste un único \(\alpha\in [0,2\pi)\), tal que \(a=\cos(\alpha)\) y \(b=\sin(\alpha)\), tal que
\[A=\begin{bmatrix}\cos(\alpha)& -\sin(\alpha)\\ \sin(\alpha)& \cos(\alpha)\end{bmatrix}.\]
Por tanto, la aplicación ortogonal es un giro, centrado en el origen, de ángulo \(\alpha\) con
\[Tr(A)=2a=2\cos(\alpha)\Rightarrow \alpha=\arccos\left(\tfrac{1}{2}Tr(A)\right)\]

Proposición: Sean \(v:(a, b)\) y \(v’:(a’, b’)\) dos puntos en el plano afín \(\mathbb{R}^2\). Si se cumple que \(a^2 + b^2 = (a’)^2 + (b’)^2\), entonces
\[
R = \begin{bmatrix} \frac{a a’ + b b’}{a^2 + b^2} & -\frac{a b’ – b a’}{a^2 + b^2} \\ \frac{a b’ – b a’}{a^2 + b^2} & \frac{a a’ + b b’}{a^2 + b^2} \end{bmatrix}
\]
realiza un giro de \((a, b)\) a \((a’, b’)\)

Giro más desplazamiento

La construcción de un «giro más desplazamiento» se conoce formalmente como movimiento rígido o isometría directa en \(\mathbb{R}^2\). En Álgebra Lineal, esto se modela de manera eficiente utilizando coordenadas homogéneas.

Un movimiento rígido es una transformación afín y se define como la combinación de una rotación y una traslación (desplazamiento):

\[
T(v) = R v + t
\]

Donde:

1. \(v\) es el vector de coordenadas originales \(\begin{bmatrix} x \\ y \end{bmatrix}\).
2. \(R\) es la matriz de giro \(2 \times 2\) (ortogonal, \(\det(R)=1\)).
3. \(t\) es el vector de traslación (desplazamiento) \(\begin{bmatrix} t_x \\ t_y \end{bmatrix}\).

De este modo, el punto girado \(v_{giro}\) se traslada por el vector \(t\):
\[
v’ = v_{giro} + t = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix},
\]

Recordad que las transformaciones afines no son transformaciones lineales, por lo que no pueden representarse con una simple multiplicación de matriz \(2 \times 2\).

Para manejar tanto la rotación (operación lineal) como la traslación (operación no lineal) con una única multiplicación matricial, se utiliza la técnica de coordenadas homogéneas en \(\mathbb{R}^3\):

\[
\begin{bmatrix} a’ \\ b’ \\ 1 \end{bmatrix} = \begin{bmatrix} \cos \theta & -\sin \theta & t_x \\ \sin \theta & \cos \theta & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} a \\ b \\ 1 \end{bmatrix}
\]

La matriz, de \(3 \times 3\), que hemos visto se denomina matriz de transformación, que combina el giro \(R\) y la traslación \(t\). En Gráficos por Computadora y Robótica, la representación con coordenadas homogéneas es el estándar porque permite concatenar (componer) múltiples giros, traslaciones y escalados con solo multiplicar las matrices de transformación homogéneas resultantes.

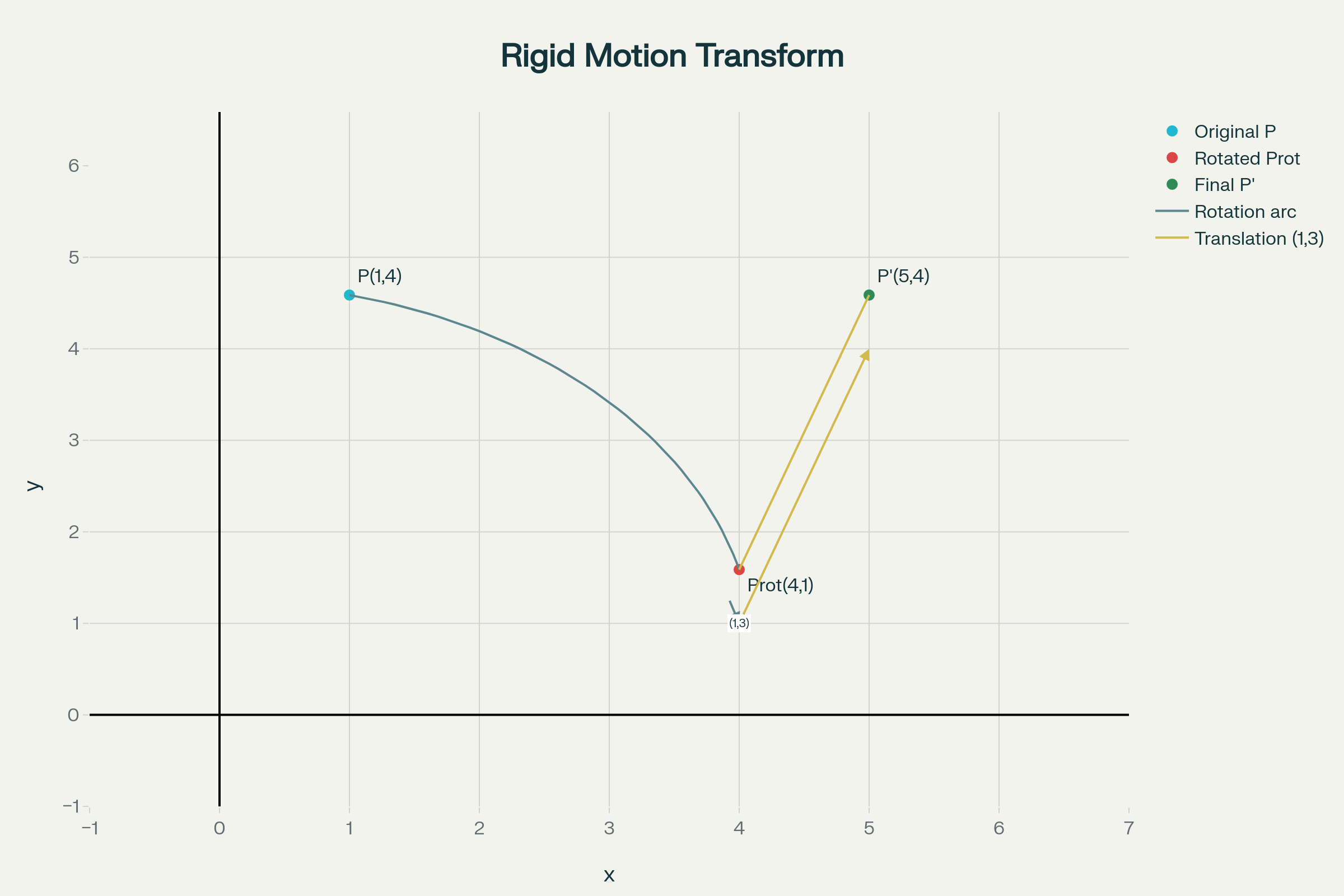
Ejemplo: Determinar el vector resultado de un giro de $90^\circ$ (\(\pi/2\) radianes) en sentido antihorario, del vector [3,2] y una traslación (desplazamiento) de [4, -1].

Solución:

Primero determinamos la matriz de giro (\(R\)):
Para \(\theta = 90^\circ\), la matriz de giro $2 \times 2$ es:
\[
R = \begin{bmatrix} \cos 90^\circ & -\sin 90^\circ \\ \sin 90^\circ & \cos 90^\circ \end{bmatrix} = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}
\]

A continuación, el vector de traslación (\(t\))
El desplazamiento es \((t_x, t_y) = (4, -1)\).

\[
t = \begin{bmatrix} 4 \\ -1 \end{bmatrix}
\]

Hacemos la Matriz de Transformación Homogénea (\(M\))
Combinamos $R$ y $t$ en una única matriz $3 \times 3$:

\[
M = \begin{bmatrix}
0 & -1 & 4 \\
1 & 0 & -1 \\
0 & 0 & 1
\end{bmatrix}
\]

Ya tenemos la matriz, ahora aplicamos la transformación con el Punto de Partida en Coordenadas Homogéneas \(v_{1, hom} = \begin{bmatrix} 3 \\ 2 \\ 1 \end{bmatrix}\):

\[
v_{2, hom} = M v_{1, hom} = \begin{bmatrix}
0 & -1 & 4 \\
1 & 0 & -1 \\
0 & 0 & 1
\end{bmatrix} \begin{bmatrix} 3 \\ 2 \\ 1 \end{bmatrix}= \begin{bmatrix} 2 \\ 2 \\ 1 \end{bmatrix}
\]

Punto Final (Vector Transformado)

\[
v_{2, hom} = \begin{bmatrix} 2 \\ 2 \\ 1 \end{bmatrix} \implies v_2 = \begin{bmatrix} 2 \\ 2 \end{bmatrix}
\]

Ejercicio: Se aplica un movimiento rígido (giro más traslación) a un punto \(P(1,4)\) del plano, transformándolo en un punto \(P'(5,4)\). Se sabe que el movimiento consiste en una rotación de ángulo $\theta$ en sentido antihorario, seguida de una traslación por el vector $t=[1,3]$. ¿Cuál es el ángulo de giro \(\theta\) en grados?

Solución:

Recordemos que la transformación afín se define mediante la fórmula:

\[
P’ = R(\theta) P + t
\]

Donde \(R(\theta) = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix}\).

Paso 1: Aislar la Rotación

Primero, despejamos la componente de rotación restando el vector de traslación \(t\) al vector final \(P’\):

\[
R(\theta) P = P’ – t
\]

Calculamos el vector de giro puro \(P_{giro} = P’ – t\):

\[
P_{giro} = \begin{bmatrix} 5 \\ 4 \end{bmatrix} – \begin{bmatrix} 1 \\ 3 \end{bmatrix} =\begin{bmatrix} 4 \\ 1 \end{bmatrix}
\]

La ecuación ahora se simplifica a:
\[
\begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} 1 \\ 4 \end{bmatrix} = \begin{bmatrix} 4 \\ 1 \end{bmatrix}
\]

Paso 2: Plantear y Resolver el Sistema

Definimos \(c = \cos \theta\) y \(s = \sin \theta\). La multiplicación matricial resulta en el siguiente sistema de ecuaciones lineales con incógnitas \(c\) y \(s\):

\[
\begin{align*} 1 \cdot c – 4 \cdot s &= 1 \quad & (E_1) \\ 4 \cdot c + 1 \cdot s &= 4 \quad & (E_2) \end{align*}
\]

Resolvemos el sistema :

\[
\begin{align*}
c &= \frac{8}{17}\\
s &= -\frac{15}{17}
\end{align*}
\]

Ya estámos en condiciones de determinar la matriz de giro y el ángulo:

Matriz de Rotación Pura \(R\)
\[
R = \begin{bmatrix} \frac{8}{17} & \frac{15}{17} \\ -\frac{15}{17} & \frac{8}{17} \end{bmatrix}
\]

Ángulo de Giro \(\theta\)
Como \(\cos \theta > 0\) y \(\sin \theta < 0\), el ángulo \(\theta\) se encuentra en el cuarto cuadrante.

\[
\theta = \arctan \left( \frac{\sin \theta}{\cos \theta} \right) = \arctan \left( \frac{-15/17}{8/17} \right) = \arctan \left( -\frac{15}{8} \right)\approx -61.9275^\circ
\]

El giro es de aproximadamente \(61.9275^\circ\) en sentido horario (negativo). Para una rotación en sentido antihorario (ángulo positivo), podemos dar el equivalente entre \(0^\circ\) y \(360^\circ\):

\[
\alpha \approx 360^\circ – 61.9275^\circ \approx 298.0725^\circ.
\]

Rotación −61.9275° (horaria) + traslación (1,3).

El escalado, en coordenadas homogéneas, lo hacemos mediante

\[
M_{escalado} = \begin{bmatrix}
s_x & 0 & 0 \\
0 & s_y & 0 \\
0 & 0 & 1
\end{bmatrix}
\]

Con esto ya podemos componer giros, traslaciones y escalados:

\[
\begin{align}
M &= M_{traslación} \cdot M_{giro} \cdot M_{escalado}\\ &= \begin{bmatrix}
1 & 0 & t_x \\
0 & 1 & t_y \\
0 & 0 & 1
\end{bmatrix}\cdot \begin{bmatrix}
c & -s & 0 \\
s & c & 0 \\
0 & 0 & 1
\end{bmatrix}\cdot \begin{bmatrix}
s_x & 0 & 0 \\
0 & s_y & 0 \\
0 & 0 & 1
\end{bmatrix}\\
&=\begin{bmatrix}
s_x c & -s_y s & t_x \\
s_x s & s_y c & t_y \\
0 & 0 & 1
\end{bmatrix}
\end{align}
\]

Donde:

• \(c = \cos \theta\)
• \(s = \sin \theta\)
• \((s_x, s_y)\) son los factores de escala.
• \((t_x, t_y)\) es el vector de traslación.

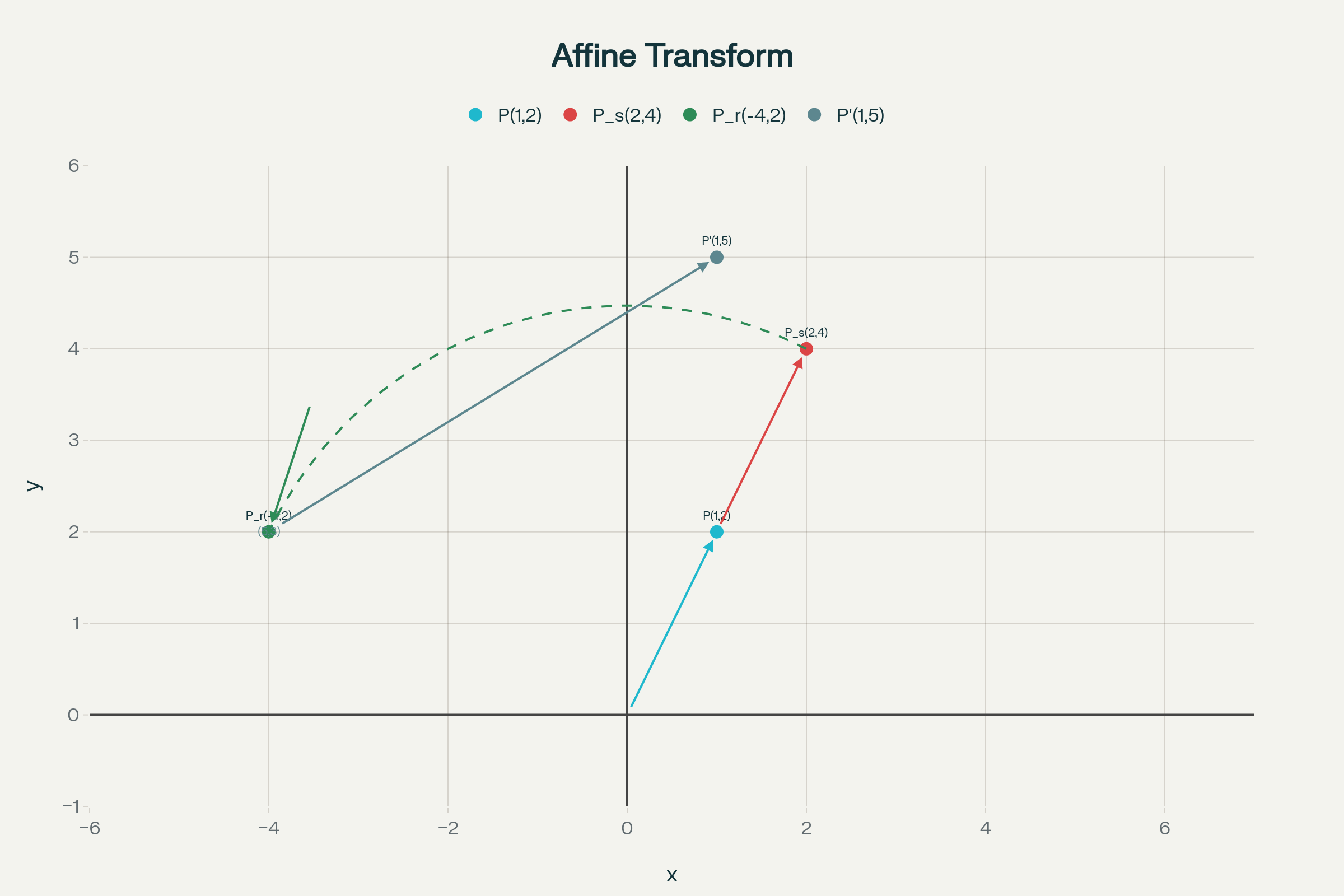
Ejemplo: Sea el punto P(1,2) al que realizamos un escalado s(2,2), un giro\(90^\circ\) antihorario y una translación por vector \(t = (5, 3)\). ¿Cuál el el punto final?

Solución:

Para trabajar más cómodos lo haremos en coordenadas homogéneas.

En coordenadas homogéneas, un punto \(P = (x, y)\) se representa como \(\tilde{P} = (x, y, 1)^T\). Las transformaciones lineales (rotación, escalado) y afines (traslación) se representan mediante matrices \(3 \times 3\).

Para el ejemplo con punto inicial \(P = (1, 2)\), las transformaciones en coordenadas homogéneas son:

1. Escalado por \(k=2\):
\[
S = \begin{bmatrix}
2 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & 1
\end{bmatrix}
\]

2. Giro \(90^\circ\) antihorario:
\[
R = \begin{bmatrix}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{bmatrix}
\]

3. Traslación por vector \(t = (5, 3)\):
\[
T = \begin{bmatrix}
1 & 0 & 5 \\
0 & 1 & 3 \\
0 & 0 & 1
\end{bmatrix}
\]

El punto final homogéneo \(\tilde{P}’\) se obtiene aplicando las transformaciones en orden (primero escalado, luego rotación, luego traslación):

\[
\tilde{P}’ = T \cdot R \cdot S \cdot \tilde{P} =
\begin{bmatrix}
1 & 0 & 5 \\
0 & 1 & 3 \\
0 & 0 & 1
\end{bmatrix}
\cdot
\begin{bmatrix}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{bmatrix}
\cdot
\begin{bmatrix}
2 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & 1
\end{bmatrix}
\cdot
\begin{bmatrix}
1 \\ 2 \\ 1
\end{bmatrix}
\]

Calculando paso a paso:

\[
S \cdot \tilde{P} =
\begin{bmatrix}
2 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 \\ 2 \\ 1
\end{bmatrix}
=
\begin{bmatrix}
2 \\ 4 \\ 1
\end{bmatrix}
\]

\[
R \cdot (S \cdot \tilde{P}) =
\begin{bmatrix}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
2 \\ 4 \\ 1
\end{bmatrix}
=
\begin{bmatrix}
-4 \\ 2 \\ 1
\end{bmatrix}
\]

\[
T \cdot (R \cdot S \cdot \tilde{P}) =
\begin{bmatrix}
1 & 0 & 5 \\
0 & 1 & 3 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
-4 \\ 2 \\ 1
\end{bmatrix}
=
\begin{bmatrix}
1 \\ 5 \\ 1
\end{bmatrix}
\]

Por lo tanto,

\[
\tilde{P}’ = \begin{bmatrix} 1 \\ 5 \\ 1 \end{bmatrix}
\]

que corresponde al punto \(P’ = (1, 5)\) en coordenadas cartesianas.

Escalado k=2 → Giro 90° → Traslación (5,3)

Simetrías

Si \(|A|=-1\), será
\[A=\begin{bmatrix}a& b\\ b& -a\end{bmatrix},\]
y habrán dos vectores \(\vec{v}_1\) y \(\vec{v}_2\), tales que \(f(\vec{v}_1)=\vec{v}_1\) y \(f(\vec{v}_2)=-\vec{v}_2\), siendo \(\vec{v}_1\bullet\vec{v}_2=0\). De este modo, la aplicación ortogonal es una simetría respecto de la recta \(r=\{\lambda\vec{v}_1;\lambda\in\mathbb{R}\}\)

Clasificación de las aplicaciones ortogonales en \(\mathbb{R}^3\)

En esta caso pueden darse cuatro matrices:

1) La matriz identidad

2) La matriz \[\begin{bmatrix}1& 0 & 0\\ 0 & 1 & 0\\ 0& 0 & -1\end{bmatrix},\] y la aplicación ortogonal es una simetría respecto del plano generado por los vectores tales que \(f(\vec{v}_1)=\vec{v}_1\) y \(f(\vec{v}_2)=\vec{v}_2\).

3) La matriz \[\begin{bmatrix}1& 0 & 0\\ 0 & \cos(\alpha) & -\sin(\alpha)\\ 0& \sin(\alpha) & \cos(\alpha)\end{bmatrix},\] y la aplicación ortogonal es un giro con eje en la recta generada por el único vector tal que \(f(\vec{v}_1)=\vec{v}_1\), y de ángulo \(\alpha\) con
\[Tr(A)=1+2\cos(\alpha)\Rightarrow \alpha=\arccos\left(\tfrac{1}{2}(Tr(A)-1)\right)\]

4) La matriz \[\begin{bmatrix}-1& 0 & 0\\ 0 & \cos(\alpha) & -\sin(\alpha)\\ 0& \sin(\alpha) & \cos(\alpha)\end{bmatrix},\] y la aplicación ortogonal es una simetría, respecto del plano generado por el ortogonal por vector tal que \(f(\vec{v}_1)=-\vec{v}_1\), compuesta con un giro de recta \(r=\{\lambda\vec{v}_1;\lambda\in\mathbb{R}\}\) y de ángulo \(\alpha\) con
\[Tr(A)=-1+2\cos(\alpha)\Rightarrow \alpha=\arccos\left(\tfrac{1}{2}(Tr(A)+1)\right)\]

Un caso particular de este último es cuando \(\alpha=\pi\), en cuyo caso \[\begin{bmatrix}-1& 0 & 0\\ 0 & -1 & 0\\ 0& 0 & -1\end{bmatrix},\] que resulta una simetría central con centro en el origen.

La justificación de lo anterior reside en el siguiente apartado de este tema, donde abordaremos los autovalores y autovectores de un endomorfismo, y, por ende, de una matriz.

Solución: