Así como la integral de una función positiva de una variable se interpreta como el área entre la gráfica de la función y el eje \({\displaystyle x}\), la integral doble de una función positiva de dos variables representa el volumen de la región entre la superficie definida por la función y el plano que contiene el dominio de la función.
Si definimos la integral doble mediante
\[\iint _{R}f(x,y)\;dxdy=\lim _{n,m\to 0}\sum _{i=0}^{n-1}\sum _{j=0}^{m-1}f(x_{ij},y_{ij})\Delta x\Delta y,\]
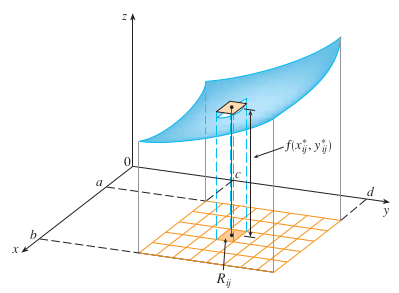
observamos que esto equivale a determinar el volumen de una función positiva \(f (x, y)\) de dos variables, definida en una región del plano \(xy\),
\[V=\iint_R f(x,y)\, dA\]
Hacemos que \(dA=dxdy\) pero no tiene por qué ser así. La integral doble así definida cumple: \[\iint_R(\lambda f(x,y)+\mu g(x,y))\,dA=\lambda\iint_R f(x,y)\,dA+\mu\iint_R g(x,y)\,dA.\]
Para calcular la integral doble utilizamos el concepto de integral iterada, de modo que
\[\iint_R f(x,y)\,dA=\int_a^b\left[\int_c^df(x,y)dy\right]dx,\] donde \(R=[a.b]\times[c,d]\).
Ejercicio: Determinar el volumen bajo la superficie de \(f(x,y)=x^2y\) en el rectángulo \(R:[1,2]\times [1,3]\)
De este modo, si existe el límite existe la integral doble, y esta se puede calcular mediante el teorema de Fubini:
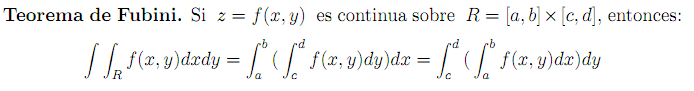
Este teorema es muy útil porque nos permite decidir qué integramos antes para facilitar el cálculo.
Ejercicio: Determinar el volumen bajo la superficie de \(f(x,y)=y\ e^{xy}\) en el rectángulo \(R:[0,1]\times [1,2]\)
Ejercicio: Sea R=[0,1]x[0,1], ¿cuál es el valor de la integral dada? \[\iint_R e^{x+y}\ dA\]
Ejercicio: Sea R=[0,1]x[0,1], ¿cuál es el valor de la integral dada? \[\iint_Rxe^{xy}\ dA\]
Nos tenemos por qué restringirnos a una región cuadrada R, podemos considerar una región plana D delimitada por curvas, las denominadas regiones de Tipo 1 y II. Así calculamos el volumen bajo una función \(z=f(x,y)\) y sobre la región D. Además, la integral doble nos permite definir el área de esa región, si queremos calcular el área encerada en D, esta será \[A(D)=\iint_D\,dA.\]
Ejercicio: Determinar el área del disco \({\displaystyle D=\{(x,y)\in \mathbb {R} ^{2}:2\leq x\leq 4\;;\;3\leq y\leq 6\}}\) encerrada por la función \(f(x,y)=cy\) donde \(c\) es una constante real
Ejercicio: ¿Cuál es el área definida mediante la recta \(y=x-1\) y la parábola \(y^2=2x+6\)?
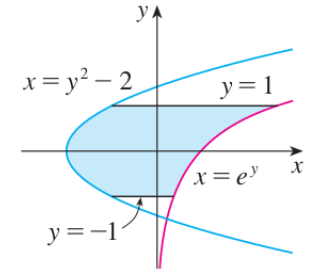
Ejercicio: ¿Cuál es el valor del área coloreada?
Bibliografía
- Capítulo 15 del libro Cálculo de varias variables, de James Stewart.
|
Ejercicio:¿Cuál es el área del disco \(D=\{(x,y);0\leq x\leq 2,x^2\leq y\leq 2x\}\)? |