Día: 4 de diciembre de 2025

Se dice que una ecuación diferencial (ED) es cualquier ecuación que contiene las derivadas de una o más variables dependientes con respecto a una o más variables independientes

Con el objetivo de referirnos a ellas, debemos clasificar las ecuaciones diferenciales
por tipo, orden y linealidad.

Si una ecuación diferencial contiene únicamente derivadas ordinarias de una o más variables dependientes con respecto a una sola variable independiente, se dice que es una ecuación diferencial ordinaria (EDO)

Para nosotros será habitual encontrarnos una ecuación diferencial(ED) como una ecuación del tipo \[F(x,y,y′,y″,\ldots,y^{(n)})=0,\]
que relaciona una variable independiente \(x\) y una función \(y=y(x)\) junto con una o más de sus derivadas.

O también, \[\frac{d^ny}{dx^n}=f(x,y,y′,y″,\ldots,y^{(n-1)})\] donde \(f\) es una función continua con valores reales,

Así nos centraremos en las EDO de la forma \[\frac{dy}{dx}=f(x,y)\ _\wedge \ \frac{d^2y}{dx^2}=f(x,y,y’)\]

Consideraremos una solución de una EDO a toda función \(\phi\), definida sobre un intervalo \(I\) y que posea al menos \(n\) derivadas continuas sobre \(I\), y que al ser sustituida en una ecuación diferencial ordinaria de
\(n\)-ésimo orden reduzca la ecuación a una identidad, se dice que es una solución de la ecuación sobre el intervalo; es decir, \[F(x,\phi(x),\phi′(x),\ldots,\phi^{(n)}(x))=0\ \forall x\in I\]

En muchos casos, esa solución, la expresamos en una relación \(G(x,y)=0\), que denominamos solución implícita, y que nos dice que existe al menos una función \(\phi\) que satisface tanto a la relación \(G(x, \phi(x)) = 0\), como la ecuación diferencial sobre un intervalo \(I\)

EDO de primer orden

Las primeras ecuaciones que trataremos son las ecuaciones diferenciales ordinarias de primer orden(EDO). Es decir, una sola variable independiente (a diferencia de las ecuaciones diferenciales parciales que involucran derivadas parciales de varias variables), y una o más de sus derivadas respecto de tal variable.

Campo de direcciones

Un campo de direcciones es una representación gráfica que nos ayuda a visualizar cómo las soluciones de una ecuación diferencial de la forma:
\[\frac{dy}{dx}=f(x,y)\]
se comportan sin resolver explícitamente la ecuación.

En esencia, el campo de direcciones asocia un pequeño segmento de línea a cada punto \((x,y)\) del plano, cuyo pendiente está determinada por el valor de \(f(x,y)\). Estas líneas indican la dirección en la que una solución de la ecuación (es decir, una curva \(y(x)\)) se movería si pasara por ese punto.

¿Por qué es importante?

1. Intuición visual: Nos permite observar cómo las soluciones de la ecuación se comportan globalmente, incluso si no sabemos calcularlas exactamente.
2. Predicción del comportamiento: Ayuda a identificar patrones, como puntos de equilibrio, ciclos o trayectorias específicas.
3. Simplificación del análisis: A veces, resolver una ecuación diferencial puede ser complicado o incluso imposible. El campo de direcciones nos proporciona información útil sobre las soluciones sin necesidad de resolverlas.

¿Cómo se construye un campo de direcciones?

• Dada la ecuación \(\frac{dy}{dx} = f(x, y)\):
  • Para cada punto del plano \((x, y)\), calcula la pendiente \(m = f(x, y)\).
  • Dibuja un pequeño segmento de recta con esa pendiente en el punto \((x, y)\).
• Ejemplo sencillo:
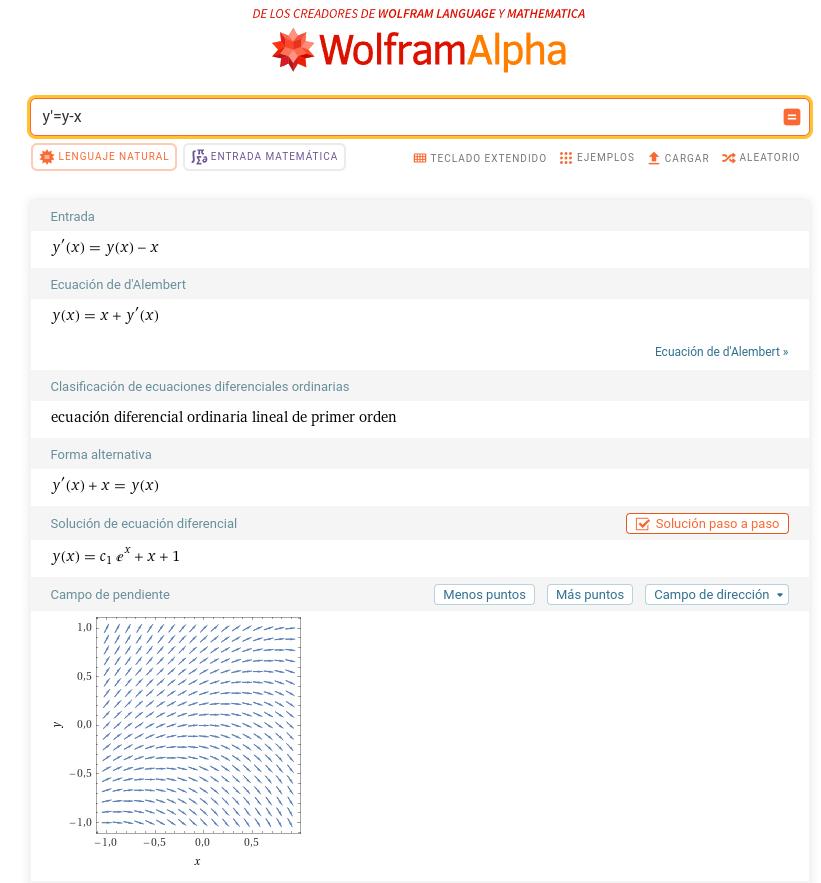
  Consideremos la ecuación \(\frac{dy}{dx} = y – x\).
  • Si \((x, y) = (0, 0)\), entonces \(f(0, 0) = 0 – 0 = 0\), y la pendiente es horizontal.
  • Si \((x, y) = (1, 2)\), entonces \(f(1, 2) = 2 – 1 = 1\), y la pendiente es 1.
  • Esto se repite para muchos puntos para construir el campo completo.
• Uso de software:
  Aunque es posible dibujar el campo de direcciones a mano, normalmente se utiliza software como Maxima, Python, MATLAB o herramientas gráficas en línea para generarlos más rápido y con mayor precisión. En Maxima, el paquete «plotdf» permite crear gráficos del campo de direcciones de una ODE unidimensional y de campos de vectores en el plano, dando la posibilidad adicional de elegir soluciones u órbitas de forma interactiva.



Primeras EDO

Las EDO que afrontaremos serán de tres tipos: la de variables separadas, las lineales de primer orden y las de Bernoulli.

La EDO más sencilla que podemos plantear es \[y’=k,\] donde \(k\) es una constante. En este caso la familia de soluciones resulta de \[y’=k\to \frac{dy}{dx}=k\to dy=kdx\to \int dy=\int kdx\to y(t)=kt+C.\] Conociendo un valor inicial \(y(t_0)=y_0\), tendremos \[y(t_0)=k\ t_0+C\to C=y_0-kt_0\to y(t)=kt+(y_0-kt_0)=k(t-t_0)+y_0.\]

Este es un caso particular del de variables separadas. Consideramos una EDO de variables separadas cuando \[\frac{dy}{dx}=\frac{f(x)}{g(y)}.\]

En este caso la solución está dada por: \[\frac{dy}{dx}=\frac{f(x)}{g(y)}\to \int g(y)\ dy=\int f(x)\ dx.\]

Ejercicio: Supongamos que una función real verifica \(\frac{dy}{dt}=e^ty\) con \(y(0)=1\) ¿cuál es el valor de \(y(1)\)?

Solución:

Vemos que es una EDO de variables separadas, pues \[\frac{dy}{dt}=e^ty\Rightarrow \frac{dy}{y}=e^t\ dt\] Ahora integramos \[\int\frac{dy}{y}=\int e^t\ dt,\] luego \[\ln|y|=e^t+C’\]
Solo nos resta despejar y tendremos \[y(t)=C\, e^{e^t}\]
La condición inicial \(y(0)=1\) implica que nuestra función es \[y(t)=e^{e^t-1}\]
Terminamos sustituyendo \(t=1\) \[y(1)=e^{e-1}=5.5749\]

---

Ejercicio: Supongamos que una función real verifica \(\frac{dy}{dt}=\frac{1}{t^2y}\) con \(y(1)=1\) ¿cuál es el valor de \(y(2)\)?

Solución:

Otra vez vemos que es una EDO de variables separadas, pues \[\frac{dy}{dt}=\frac{1}{t^2y}\Rightarrow {y}\ {dy}=\frac{dt}{t^2}\] Ahora integramos \[\int{y}\ {dy}=\int\frac{dt}{t^2},\] luego \[\frac{y^2}{2}=C’-\frac{1}{t}\]
La condición inicial \(y(1)=1\) implica que nuestra función es \[\frac{{{y}^{2}}}{2}=\frac{3 t-2}{2 t}\]
Terminamos sustituyendo \(t=2\) \[\frac{{{y}^{2}}}{2}=1\Rightarrow y=\pm \sqrt{2}\]

---

Ejercicio: Supongamos que una función real verifica \(\frac{dy}{dt}=ty+t\) con \(y(0)=1\) ¿cuál es el valor de \(y(1)\)?

Solución:

De nuevo es una EDO de variables separadas, pues \[\frac{dy}{dt}=ty+t\Rightarrow \frac{dy}{y+1}=tdt\] Ahora integramos \[\int\frac{dy}{y+1}=\int tdt,\] luego \[\ln|y+1|=\frac{t^2}{2}+C’\]
Solo nos resta despejar y tendremos \[y(t)=C\, {e}^{\frac{t^2}{2}}-1\]
La condición inicial \(y(0)=1\) implica que nuestra función es \[y(t)=2{e}^{\frac{t^2}{2}}-1\]
Terminamos sustituyendo \(t=1\) \[y(1)=2{e}^{\frac{1}{2}}-1=2\sqrt{e}-1=2.2974\]

---

Bibliografía

• Capítulo 7 del libro Biocalculus: Calculus for Life Sciences, de James Stewart.

---

Ejercicio: El número de bacterias en un cultivo viene dado por una solución de la ecuación \[y’=2y,\] siendo \(y\) una función que depende de la variable independiente \(t\) (que no aparece explícitamente), que representa el tiempo medido en horas. Supongamos que se realiza un experimento comenzando con una población de 100 bacterias en el instante \(t=0\). Podemos decir que 4 horas después de comenzar el experimento, el número de bacterias presentes en el cultivo habrá aumentado hasta

100001 298095 463000

Solución:

B.)